
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:
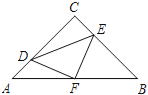
①△DFE是等腰直角三角形;
②四边形CDFE不可能为正方形,
③DE长度的最小值为4;
④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为8.
其中正确的结论是( )
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
【答案】B
【解析】试题分析:解此题的关键在于判断△DEF是否为等腰直角三角形,作常规辅助线连接CF,由SAS定理可证△CFE和△ADF全等,从而可证∠DFE=90°,DF=EF.所以△DEF是等腰直角三角形.可证①正确,②错误,再由割补法可知④是正确的;
判断③,⑤比较麻烦,因为△DEF是等腰直角三角形DE=![]() DF,当DF与BC垂直,即DF最小时,DE取最小值4
DF,当DF与BC垂直,即DF最小时,DE取最小值4![]() ,故③错误,△CDE最大的面积等于四边形CDEF的面积减去△DEF的最小面积,由③可知⑤是正确的.故只有①④⑤正确.
,故③错误,△CDE最大的面积等于四边形CDEF的面积减去△DEF的最小面积,由③可知⑤是正确的.故只有①④⑤正确.
解:连接CF;
∵△ABC是等腰直角三角形,
∴∠FCB=∠A=45°,CF=AF=FB;
∵AD=CE,
∴△ADF≌△CEF(SAS);
∴EF=DF,∠CFE=∠AFD;
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFD=∠EFD=90°,
∴△EDF是等腰直角三角形(故①正确).
当D、E分别为AC、BC中点时,四边形CDFE是正方形(故②错误).
∵△ADF≌△CEF,
∴S△CEF=S△ADF∴S四边形CEFD=S△AFC,(故④正确).
由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小;
即当DF⊥AC时,DE最小,此时DF=![]() BC=4.
BC=4.
∴DE=![]() DF=4
DF=4![]() (故③错误).
(故③错误).
当△CDE面积最大时,由④知,此时△DEF的面积最小.
此时S△CDE=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8(故⑤正确).
故选:B.


科目:初中数学 来源: 题型:
【题目】下面说法中正确的是( )
A. -2-1-3可以说是-2,-1,-3的和
B. -2-1-3可以说是2,-1,-3的和
C. -2-1-3是连减运算不能说成和
D. -2-1-3=-2+3-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A、平移或旋转后的图形的形状大小不变
B、平移过程中对应线段平行(或在同一条直线上)且相等
C、旋转过程中,图形中的每一点都旋转了相同的路程
D、旋转过程中,对应点到旋转中心的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组数中,以a,b,c为边的三角形不是直角三角形的是()
A.a=1.5,b=2,c=3B.a=7,b=24,c=25
C.a=6,b=8,c=10D.a=5,b=12,c=13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适合用普查的是( )
A.了解我省初中学生的家庭作业时间B.了解“嫦娥四号”卫星零部件的质量
C.了解一批电池的使用寿命D.了解某市居民对废电池的处理情况
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com