
【题目】如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,且![]() 于D,与⊙O交于点F.
于D,与⊙O交于点F.
(1)判断AC是否是∠DAE的平分线?并说明理由;
(2)连接OF与AC交于点G,当AG=GC=1时,求切线![]() 的长.
的长.

【答案】(1) AC是∠DAE的平分线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)连接OC,根据切线的性质可得OC⊥DE,又AD⊥DE,得出AD∥OC,根据圆的半径相等得出∠1=∠OCA,再由平行线的性质得出∠2=∠OCA,等量代换即可得出结论;
(2)先证明△AOF是等边三角形,进而得出∠DAO=60°,由(1)中结论可得∠1=30°,根据直角三角形的两锐角互余可得∠E=30°,所以∠1=∠E,根据等角对等边得出CE=AC,即可得到答案.
试题解析:
解:(1)AC是∠DAE的平分线.
证明:连接![]() .
.
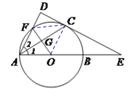
∵DE是⊙O的切线,∴OC⊥DE,.
∵AD⊥DE,∴∠ADC=∠OCE=![]() ,
,
∴AD∥OC,.
∴∠2=∠ACO,∵OA=OC,∴∠1=∠ACO,
∴∠1=∠2,∴AC是∠DAE的平分线.
(2)∵![]() =1 , ∴
=1 , ∴![]() ,即
,即![]() .
.
又∠1=∠2, ![]()
![]() , ∴
, ∴![]()
又![]() ,
, ![]() ∴△
∴△![]() 是等边三角形,
是等边三角形,
![]() ,
, ![]() ,.
,.
又∠ADE=![]() ,
,
∴![]() .
.
∴CE=AC=AG+CG=2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
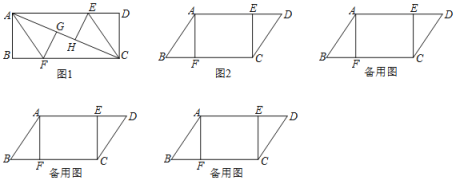
【题目】(1)如图1,长方形ABCD中分别沿AF、CE将AC两侧折叠,使点B、D分别落在AC上的G、H处,则线段AE______CF.(填“>”“<”或“=”)
(2)如图2,在平行四边形ABCD中,△ABF≌△CDE,AB=10cm,BF=6cm,AF=8cm,动点P、Q分别从A、C两点同时出发,点P自A→F→B→A停止,点Q自C→D→E→C停止.
①若点P的速度为每秒5cm,点Q的速度为每秒4cm,设运动时间为t秒.当点P在FB上运动,而点Q在DE上运动时,若四边形APCQ是平行四边形,求此时t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),利用备用图探究,当a与b满足什么数量关系时,四边形APCQ是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱,各种品牌相继投放市场,一汽贸公司经销某品牌新能源汽车,去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1﹣5月份每辆车的销售价格是多少万元?设今年1﹣5月份每辆车的销售价格为x万元.则根据题意,可列方程____________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2(k+1)x+k2﹣2k﹣3与x轴有两个交点.
(Ⅰ)求k取值范围;
(Ⅱ)当k取最小整数时,此二次函数的对称轴和顶点坐标;
(Ⅲ)将(Ⅱ)中求得的抛物线在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象.请你求出新图象与直线y=x+m有三个不同公共点时m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买20张课桌和一批椅子,该校了解到甲、乙两家商场以同样的价格出售同一型号的课桌与椅子,课桌报价200元/张,椅子报价50元/把.甲、乙两商场分别给出了不同的优惠方案.甲商场的优惠方案:凡买一张课桌赠送一把椅子;乙商场的优惠方案:所有课桌和椅子均按报价的九折销售.若该校需要![]() 把椅子,在甲商场购买所花费用为
把椅子,在甲商场购买所花费用为![]() (元),在乙商场购买所花总费用为
(元),在乙商场购买所花总费用为![]() (元).
(元).
(1)请分别写出![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)该校计划用8100元购买课桌和椅子,选甲、乙哪一家商场可以购买到尽可能多的椅子,说明理由;
(3)该校选择甲、乙哪一家商场花费较少?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系(每格的宽度为1)中,已知点A的坐标是![]() ,点B的坐标是
,点B的坐标是![]() ,
,

![]()
(1)在直角坐标平面中画出线段AB;
(2)B点到原点O的距离是 ;
(3)将线段AB沿![]() 轴的正方向平移4个单位,画出平移后的线段A1BI,并写出点A1、B1的坐标.
轴的正方向平移4个单位,画出平移后的线段A1BI,并写出点A1、B1的坐标.
(4)求△A1B B1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com