
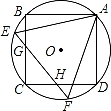
如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则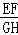 的值是( )
的值是( )
A.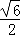 B.
B.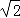 C.
C.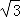 D.2
D.2
C【考点】正多边形和圆.
【专题】压轴题.
【分析】首先设⊙O的半径是r,则OF=r,根据AO是∠EAF的平分线,求出∠COF=60°,在Rt△OIF中,求出FI的值是多少;然后判断出OI、CI的关系,再根据GH∥BD,求出GH的值是多少,再用EF的值比上GH的值,求出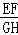 的值是多少即可.
的值是多少即可.
【解答】解:如图,连接AC、BD、OF, ,
,
设⊙O的半径是r,
则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴FI=r•sin60°= ,
,
∴EF= ,
,
∵AO=2OI,
∴OI= ,CI=r﹣
,CI=r﹣ =
= ,
,
∴ ,
,
∴ ,
,
∴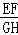 =
= ,
,
即则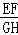 的值是
的值是 .
.
故选:C.
【点评】此题主要考查了正多边形与圆的关系,要熟练掌握,解答此题的关键是要明确正多边形的有关概念:①中心:正多边形的外接圆的圆心叫做正多边形的中心.②正多边形的半径:外接圆的半径叫做正多边形的半径.③中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.④边心距:中心到正多边形的一边的距离叫做正多边形的边心距.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=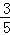 ,求⊙O半径的长.
,求⊙O半径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
某足球队在4场足球赛中战绩是:第一场3:2胜,第二场2:3负,第三场1:1平,第四场4:5负,则该队在这次比赛中总的净胜球数是( )
A.﹣2 B.﹣1 C.+1 D.+2
查看答案和解析>>
科目:初中数学 来源: 题型:
设同一个圆的内接正六边形、正八边形、正十二边形的边心距分别为r6,r8,r12,则r6,r8,r12的大小关系为( )
A.r6>r8>r12 B.r6<r8<r12 C.r8>r6>r12 D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
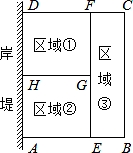
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
将一根长 24cm 的筷子置于底面直径为 5cm,高为 12cm 的圆柱形水杯中,如图所示,设筷子露 出在杯子外面长为 hcm,你能求出 h 的取值范围吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com