
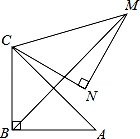
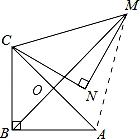
如图,在Rt△ABC中,∠ABC=90°,AB=BC= ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
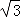 +1 .
+1 .
【考点】旋转的性质;全等三角形的判定与性质;角平分线的性质;等边三角形的判定与性质;等腰直角三角形.
【专题】压轴题.
【分析】如图,连接AM,由题意得:CA=CM,∠ACM=60°,得到△ACM为等边三角形根据AB=BC,CM=AM,得出BM垂直平分AC,于是求出BO=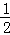 AC=1,OM=CM•sin60°=
AC=1,OM=CM•sin60°=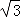 ,最终得到答案BM=BO+OM=1+
,最终得到答案BM=BO+OM=1+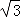 .
.
【解答】解:如图,连接AM,
由题意得:CA=CM,∠ACM=60°,
∴△ACM为等边三角形,
∴AM=CM,∠MAC=∠MCA=∠AMC=60°;
∵∠ABC=90°,AB=BC= ,
,
∴AC=2=CM=2,
∵AB=BC,CM=AM,
∴BM垂直平分AC,
∴BO=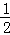 AC=1,OM=CM•sin60°=
AC=1,OM=CM•sin60°=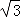 ,
,
∴BM=BO+OM=1+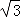 ,
,
故答案为:1+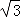 .
.
【点评】本题考查了图形的变换﹣旋转,等腰直角三角形的性质,等边三角形的判定和性质,线段的垂直平分线的性质,准确把握旋转的性质是解题的关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,抛物线 与x轴交于点A(
与x轴交于点A( ,0)、B(4,0)两点,与y轴交于点C.
,0)、B(4,0)两点,与y轴交于点C.
(1)求抛物线的表达式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度向C点运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使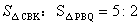 ,求K点坐标.
,求K点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求证:方程总有两个不相等的实数根.
(2)设方程的两根为x1,x2(x1<x2),则当0≤p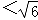 时,请直接写出x1和x2的取值范围.
时,请直接写出x1和x2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下.将0.000075用科学记数法表示为……………………………( )
A.7.5×105 B.7.5×10-5 C.0.75×10-4 D.75×10-6
查看答案和解析>>
科目:初中数学 来源: 题型:
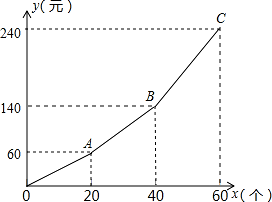
某加工厂为赶制一批零件,通过提高加工费标准的方式调动工人积极性.工人每天加工零件获 得的加工费 y(元)与加工个数 x(个)之间的函数图象为折线 OA﹣AB﹣BC,如图所示.
(1)求工人一天加工零件不超过 20 个时每个零件的加工费. 求 40≤x≤60 时 y 与 x 的函数关系式.
(3)小王两天一共加工了 60 个零件,共得到加工费 220 元.在这两天中,小王第一天加工的零件
不足 20 个,求小王第一天加工零件的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com