
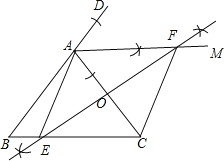
【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实验与操作:
根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)

(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
【答案】(1)作图见解析;(2)四边形AECF的形状为菱形.
【解析】
试题分析:先作以个角的交平分线,再作线段的垂直平分线得到几何图形,由AB=AC得∠ABC=∠ACB,由AM平分∠DAC得∠DAM=∠CAM,则利用三角形外角性质可得∠CAM=∠ACB,再根据线段垂直平分线的性质得OA=OC,∠AOF=∠COE,于是可证明△AOF≌△COE,所以OF=OE,然后根据菱形的判定方法易得四边形AECF的形状为菱形.
解:如图所示,
四边形AECF的形状为菱形.理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
∵AM平分∠DAC,
∴∠DAM=∠CAM,
而∠DAC=∠ABC+∠ACB,
∴∠CAM=∠ACB,
∴EF垂直平分AC,
∴OA=OC,∠AOF=∠COE,
在△AOF和△COE中
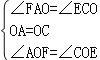 ,
,
∴△AOF≌△COE,
∴OF=OE,
即AC和EF互相垂直平分,
∴四边形AECF的形状为菱形.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 有一个角为直角的四边形是菱形
B. 对角线互相垂直的菱形是正方形
C. 对角线相等的平行四边形是矩形
D. 一组邻边相等的平行四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年,长沙地铁2号线的开通运营,极大地缓解了城市中心的交通压力,为我市再次获评“中国最具幸福感城市”提供了有力支撑.据统计,长沙地铁2号线每天承运力约为185 000人次,则数据185 000用科学记数法表示为( )
A. 1.85×105 B. 1.85×104
C. 1.8×105 D. 18.5×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x+4)(x﹣6)与x轴交于A,B两点(点A在B的左侧),顶点为P,且点P在直线y=2x+m上.
(1)试用含m的代数式表示a;
(2)若△ABP为直角三角形,试求该抛物线和直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A. 96 B. 69 C. 66 D. 99
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)|-1|+(—2)3+(7-π)0-(![]() )-1;
)-1;
(2) (-2a)3·(a2)2÷a3
(3) (3a+b-2)(3a-b+2)
(4)10002-1002×998
(5) (x+1)(x2+1)(x4+1)(x-1)
(6) (3a+2)2(3a-2)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com