
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
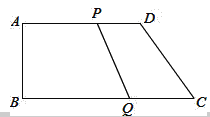
(1)BC= cm;
(2)当t为多少时,四边形PQCD成为平行四边形?
(3)当t为多少时,四边形PQCD为等腰梯形?
(4)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若不存在,说明理由.
【答案】(1)18;(2)当t=![]() 秒时四边形PQCD为平行四边形;(3)当t=
秒时四边形PQCD为平行四边形;(3)当t=![]() 时,四边形PQCD为等腰梯形;(4)存在t, t的值为
时,四边形PQCD为等腰梯形;(4)存在t, t的值为![]() 秒或4秒或
秒或4秒或![]() 秒.
秒.
【解析】试题分析:(1)作DE⊥BC于E,则四边形ABED为矩形.在直角△CDE中,已知DC、DE的长,根据勾股定理可以计算EC的长度,根据BC=BE+EC即可求出BC的长度;
(2)由于PD∥QC,所以当PD=QC时,四边形PQCD为平行四边形,根据PD=QC列出关于t的方程,解方程即可;
(3)首先过D作DE⊥BC于E,可求得EC的长,又由当PQ=CD时,四边形PQCD为等腰梯形,可求得当QC-PD=QC-EF=QF+EC=2CE,即3t-(12-2t)=12时,四边形PQCD为等腰梯形,解此方程即可求得答案;
(4)因为三边中,每两条边都有相等的可能,所以应考虑三种情况.结合路程=速度×时间求得其中的有关的边,运用等腰三角形的性质和解直角三角形的知识求解.
试题解析:根据题意得:PA=2t,CQ=3t,则PD=AD-PA=12-2t.
(1)如图,过D点作DE⊥BC于E,则四边形ABED为矩形,
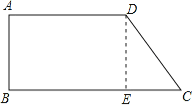
DE=AB=8cm,AD=BE=12cm,
在直角△CDE中,∵∠CED=90°,DC=10cm,DE=8cm,
∴EC=![]() =6cm,
=6cm,
∴BC=BE+EC=18cm.
(2)∵AD∥BC,即PD∥CQ,
∴当PD=CQ时,四边形PQCD为平行四边形,
即12-2t=3t,
解得t=![]() 秒,
秒,
故当t=![]() 秒时四边形PQCD为平行四边形;
秒时四边形PQCD为平行四边形;
(3)如图,过D点作DE⊥BC于E,则四边形ABED为矩形,DE=AB=8cm,AD=BE=12cm,
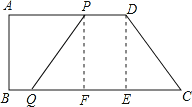
当PQ=CD时,四边形PQCD为等腰梯形.
过点P作PF⊥BC于点F,过点D作DE⊥BC于点E,则四边形PDEF是矩形,EF=PD=12-2t,PF=DE.
在Rt△PQF和Rt△CDE中,
![]() ,
,
∴Rt△PQF≌Rt△CDE(HL),
∴QF=CE,
∴QC-PD=QC-EF=QF+EC=2CE,
即3t-(12-2t)=12,
解得:t=![]() ,
,
即当t=![]() 时,四边形PQCD为等腰梯形;
时,四边形PQCD为等腰梯形;
(4)△DQC是等腰三角形时,分三种情况讨论:
①当QC=DC时,即3t=10,
∴t=![]() ;
;
②当DQ=DC时, ![]()
∴t=4;
③当QD=QC时,3t×![]()
∴t=![]() .
.
故存在t,使得△DQC是等腰三角形,此时t的值为![]() 秒或4秒或
秒或4秒或![]() 秒.
秒.


科目:初中数学 来源: 题型:
【题目】在△ABC中,点D在边BA或BA的延长线上,过点D作DE∥BC,交∠ABC的角平分线于点E.
(1)如图1,当点D在边BA上时,点E恰好在边AC上,求证:∠ADE=2∠DEB;
(2)如图2,当点D在BA的延长线上时,请直接写出∠ADE与∠DEB之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队要进行一次急行军训练,路程为32km.大部队先行,出发1小时后,由特种兵组成的突击小队才出发,结果比大部队提前20分钟到达目的地.已知突击小队的行进速度是大部队的1.5倍.
(1)求大部队的行进速度.(列方程解应用题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A. 得分在70~80分之间的人数最多
B. 该班的总人数为40
C. 得分在90~100分之间的人数最少
D. 及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长均为1的7×7网格图中,格点上有A,B,C,D,E五个定点,如图所示,一个动点P从点E出发,绕点A逆时针旋转90°,之后该动点继续绕点B,C,D逆时针90°后回到初始位置,点P运转路线的总长是 . (结果保留π)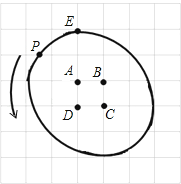
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点B、E、C、F在一条直线上,AB = DF,AC = DE,BE = CF.
求证: (1) △ABC ≌ △DFE ;
(2)连接AF、BD,求证:四边形ABDF是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=![]() ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC的周长是32,以它的三边中点为顶点组成第2个三角形,再以第2个三角形的三边中点为顶点组成的第3个三角形,…,则第n个三角形的周长为 . 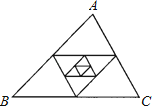
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负.![]() 年
年![]() 月
月![]() 日他办理了
日他办理了![]() 件业务:
件业务:![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元.
元.
![]() 若他早上领取备用金
若他早上领取备用金![]() 元,那么下班时应交回银行多少元?
元,那么下班时应交回银行多少元?
![]() 若每办一件业务,银行发给业务量的
若每办一件业务,银行发给业务量的![]() 作为奖励,那么这天小张应得奖金多少元?
作为奖励,那么这天小张应得奖金多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com