
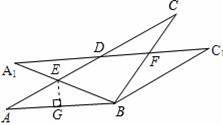
在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0<α<120°),得△A1BC1,交AC于点E,AC分别交A1C1、BC于D、F两点.


(1)如图①,观察并猜想,在旋转过程中,线段EA1与FC有怎样的数量关系?并证明你的结论;
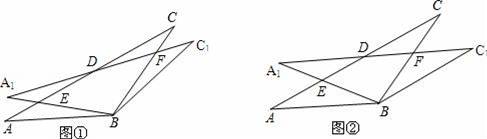
(2)如图②,当α=30°时,试判断四边形BC1DA的形状,并说明理由;
(3)在(2)的情况下,求ED的长.
【考点】旋转的性质;全等三角形的判定与性质;菱形的判定;解直角三角形.
【专题】几何综合题.
【分析】(1)根据等边对等角的性质可得∠A=∠C,再根据旋转的性质可得∠ABE=∠C1BF,AB=BC=A1B=BC1,然后利用“角边角”证明△ABE和△C1BF全等,根据全等三角形对应边相等可得BE=BF,从而得解;
(2)先根据旋转的性质求出∠ABC1=150°,再根据同旁内角互补,两直线平行求出AB∥C1D,AD∥BC1,证明四边形BC1DA是平行四边形,又因为邻边相等,所以四边形BC1DA是菱形;
(3)过点E作EG⊥AB于点G,等腰三角形三线合一的性质可得AG=BG=1,然后解直角三角形求出AE的长度,再利用DE=AD﹣AE计算即可得解.
【解答】解:(1)EA1=FC.理由如下:
∵AB=BC,∴∠A=∠C,
∵△ABC绕点B顺时针旋转角α得△A1BC1,
∴∠ABE=∠C1BF,AB=BC=A1B=BC1,
在△ABE和△C1BF中,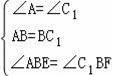
 ,
,
∴△ABE≌△C1BF(ASA),
∴BE=BF,
∴A1B﹣BE=BC﹣BF,
即EA1=FC;
(2)四边形BC1DA是菱形.理由如下:
∵旋转角α=30°,
∠ABC=120°,
∴∠ABC1=∠ABC+α
=120°+30°=150°,
∵∠ABC=120°,AB=BC,
∴∠A=∠C=
 (180°﹣120°)=30°,
(180°﹣120°)=30°,
∴∠ABC1+∠C1=150°+30°=180°,
∠ABC1+∠A=150°+30°=180°,
∴AB∥C1D,AD∥BC1,
∴四边形BC1DA是平行四边形,
又∵AB=BC1,
∴四边形BC1DA是菱形;
(3)过点E作EG⊥AB,
∵∠A=∠ABA1=30°,
∴AG=BG=
 AB=1,
AB=1,
在Rt△AEG中,AE=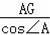
 =
=
 =
=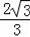
 ,
,
由(2)知AD=AB=2,
∴DE=AD﹣AE=2﹣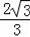
 .
.


【点评】本题考查了旋转的性质,主要利用了全等三角形的判定与性质,菱形的判定与性质,以及解直角三角形,等腰三角形三线合一的性质,难度不大,利用好旋转变换只改变图形的位置不改变图形的形状与大小,找出相等的线段是解题的关键.


科目:初中数学 来源: 题型:
下列条件之一能使菱形ABCD是正方形的为( )

①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD.
A.①③ B.②③ C.②④ D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二元一次方程x+y=1,下列说法不正确的是( ).
(A)它有无数多组解 (B) 它只有一组非负整数解
(C) 它有无数多组整数解 (D)它没有正整数解
查看答案和解析>>
科目:初中数学 来源: 题型:
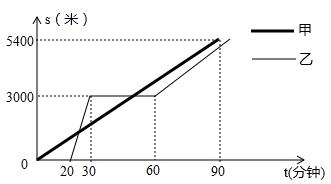
某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据以上信息回答下列问题:
(1)乙出发后多长时间与甲相遇?
(2)要使甲到达景点C时,乙与C的路程不超过400米,则乙从景点B步行到景点C的速度至少为多少?(结果精确到0.1米/分钟)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com