
 如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | 2 | D. | 3 |
分析 因为PQ为切线,所以△OPQ是直角三角形,又因为OQ为定值,所以当OP最小时,PQ最小;根据垂线段最短,知OP=3时PQ最小;根据勾股定理求出PQ的最小值.
解答 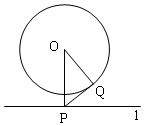 解:过点O作直线l的垂线,垂足为P,过P作⊙O的切线PQ,切点为Q,连接OQ,此时PQ为最小,
解:过点O作直线l的垂线,垂足为P,过P作⊙O的切线PQ,切点为Q,连接OQ,此时PQ为最小,
∴OP=3,OQ=2,
∵PQ切⊙O于点Q,
∴∠OQP=90°,
由勾股定理得:PQ=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
则PQ的最小值为$\sqrt{5}$,
故选A.
点评 本题考查了切线的性质、点到直线的距离,熟练掌握圆的切线垂直于经过切点的半径;本题也是求最值问题,利用数形结合,发现PQ在直角三角形OPQ中,所以PQ的最小值,与另两边OP和OQ有关,由此来判断最小值时点P的位置.


科目:初中数学 来源: 题型:解答题
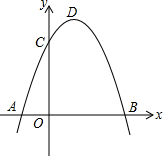 如图,抛物线y=-x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.
如图,抛物线y=-x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+2)2+3 | B. | y=(x+2)2-3 | C. | y=(x-2)2+3 | D. | y=(x-2)2-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
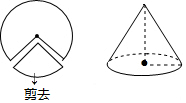 如图,从半径为9cm的圆形纸片中剪去一个扇形,使剪去的扇形的弧长为圆周长的$\frac{1}{3}$,将留下的扇形纸片围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )
如图,从半径为9cm的圆形纸片中剪去一个扇形,使剪去的扇形的弧长为圆周长的$\frac{1}{3}$,将留下的扇形纸片围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )| A. | 6cm | B. | 3$\sqrt{5}$cm | C. | 8cm | D. | 5$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com