
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当![]() = 时,四边形ADFE是平行四边形.
= 时,四边形ADFE是平行四边形.
【答案】![]()
【解析】解:当![]() =
=![]() 时,四边形ADFE是平行四边形.
时,四边形ADFE是平行四边形.
理由:∵![]() =
=![]() ,
,
∴∠CAB=30°,
∵△ABE为等边三角形,EF⊥AB,
∴EF为∠BEA的平分线,∠AEB=60°,AE=AB,
∴∠FEA=30°,又∠BAC=30°,
∴∠FEA=∠BAC,
在△ABC和△EAF中,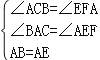 ,
,
∴△ABC≌△EAF(AAS);
∵∠BAC=30°,∠DAC=60°,
∴∠DAB=90°,即DA⊥AB,
∵EF⊥AB,
∴AD∥EF,
∵△ABC≌△EAF,
∴EF=AC=AD,
∴四边形ADFE是平行四边形.
故答案为:![]() .
.
由三角形ABE为等边三角形,EF垂直于AB,利用三线合一得到EF为角平分线,得到∠AEF=30°,进而确定∠BAC=∠AEF,再由一对直 角相等,及AE=AB,利用AAS即可得证△ABC≌△EAF;由∠BAC与∠DAC度数之和为90°,得到DA垂直于AB,而EF垂直于AB,得到EF 与AD平行,再由全等得到EF=AC,而AC=AD,可得出一组对边平行且相等,即可得证.


科目:初中数学 来源: 题型:
【题目】如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣ ![]() ,3),反比例函数y=
,3),反比例函数y= ![]() 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( ) 
A.4 ![]()
B.﹣4 ![]()
C.2 ![]()
D.﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1﹣![]() ,1+
,1+![]() )在双曲线y=
)在双曲线y=![]() (x<0)上.
(x<0)上.
(1)求k的值;
(2)在y轴上取点B(0,1),为双曲线上是否存在点D,使得以AB,AD为邻边的平行四边形ABCD的顶点C在x轴的负半轴上?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1 , A2依次在y=![]() (x>0)的图象上,点B1 , B2依次在x轴的正半轴上.若△A1OB1 , △A2B1B2均为等边三角形,则点B2的坐标为 .
(x>0)的图象上,点B1 , B2依次在x轴的正半轴上.若△A1OB1 , △A2B1B2均为等边三角形,则点B2的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.
(1)每个气排球和每个篮球的价格各是多少元?
(2)该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,应选择哪种购买方案可使总费用最低?最低费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com