
【题目】如图, △ABC内接于⊙O, AD⊥BC于D, AE是⊙O的直径. 若AB=6, AC=8, AE=11, 求AD的长.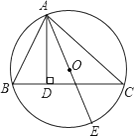
【答案】解:连接CE,则∠E=∠B,
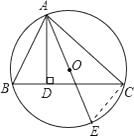
∵AE是⊙O的直径,
∴∠ACE=90°,
又∵AD⊥BC,
∴∠ACE=∠ADB=90°,
∴△ACE∽△ADB,
∴ ![]() ,
,
即 ![]() ,
,
解得AD= ![]()
【解析】根据直径所对的圆周角是直角,得到∠ACE=90°,由AD⊥BC,得到△ACE∽△ADB,得到比例,求出AD的值.
【考点精析】根据题目的已知条件,利用圆周角定理和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】已知![]() ,对角线AC、BD相交于点O.
,对角线AC、BD相交于点O.
⑴若AB=BC,则![]() 是_______.
是_______.
⑵若AC=BD,则![]() 是_________.
是_________.
⑶若∠BCD=90°,则![]() 是_________.
是_________.
⑷若OA=OB,且OA⊥OB,则![]() 是_________.
是_________.
⑸若AB=BC,且AC=BD,则![]() 是_________.
是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好地推进太原市生活垃圾分类工作,改善城市生态环境,2019年12月17日,太原市政府召开了太原市生活垃圾分类推进会,意味着太原垃圾分类战役的全面打响.某小区准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该小区物业计划用不多于2100元的资金购买A、B两种型号的垃圾箱共20个,则该小区最多可以购买B型垃圾箱多少个?
(3)在(2)的条件下,要求至少购买3个B型垃圾箱,请设计出最省钱的购买方案,并求出最少购买费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探索:
已知点O为直线AB上一点,作射线OC,将直角三角板ODE放置在直线上方(如图①),使直角顶点与点O重合,一条直角边OD重叠在射线OA上,将三角板绕点O旋转

(1)当三角板旋转到如图②的位置时,若OD平分∠AOC,试说明OE也平分∠BOC.
(2)若OC⊥AB,垂足为点O(如图③),请直接写出与∠DOB互补的角
(3)若∠AOC=135°(如图④),三角板绕点O按顺时针从如图①的位置开始旋转,到OE边与射线OB重合结束. 请通过操作,探索:在旋转过程中,∠DOB![]() ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】木工师傅要做一个如图所示的窗框,上半部分是半圆,下半部分为六个大小一样的长方形,长方形的长和宽的比为![]() .请你帮他计算:
.请你帮他计算:
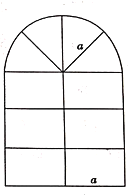
(1)设长方形的长为![]() 米,用含
米,用含![]() 的代数式表示所需材料的长度为 (结果保留
的代数式表示所需材料的长度为 (结果保留![]() ,重合部分忽略不计)
,重合部分忽略不计)
(2)当长方形的长为![]() 米时,所需材料的长度是多少?(精确到
米时,所需材料的长度是多少?(精确到![]() 米,其中
米,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com