
����Ŀ��������̽����
��֪��OΪֱ��AB��һ�㣬������OC����ֱ�����ǰ�ODE������ֱ������(��ͼ��)��ʹֱ�Ƕ������O�غϣ�һ��ֱ�DZ�OD�ص�������OA�ϣ������ǰ��Ƶ�O��ת

��1�������ǰ���ת����ͼ����λ��ʱ����ODƽ����AOC����˵��OEҲƽ����BOC.
��2����OC��AB������Ϊ��O(��ͼ��)����ֱ��д������DOB�����Ľ�
��3������AOC=135��(��ͼ��)�����ǰ��Ƶ�O��˳ʱ������ͼ����λ�ÿ�ʼ��ת����OE��������OB�غϽ���. ��ͨ��������̽��������ת�����У���DOB![]() ��COE�IJ��Ƿ����仯�������䣬����������ֵ�����仯�����ú���n(nΪ���ǰ���ת�Ķ���)�Ĵ���ʽ��ʾ�����.
��COE�IJ��Ƿ����仯�������䣬����������ֵ�����仯�����ú���n(nΪ���ǰ���ת�Ķ���)�Ĵ���ʽ��ʾ�����.
���𰸡���1����ODƽ����AOC�ɵ���AOD=��COD������DOE=90���ɵ���AOD+��EOB=90������COD+��COE=90��������֤�ý�������2����AOD����COE��
��3������n��45������DOB![]() ��COE=135��������n��45������DOB
��COE=135��������n��45������DOB![]() ��COE=225��
��COE=225��![]() 2n
2n
��������
�����������1����ODƽ����AOC�ɵ���AOD=��COD������DOE=90���ɵ���AOD+��EOB=90������COD+��COE=90��������֤�ý��ۣ�
��2����OC��AB�ɵ���AOD+��COD=90��������DOE=90���ɵ���COD+��COE=90�������ɵõ���AOD=��COE���Ӷ������������DOB�����Ľǣ�
��3��������ת45��ʱ��OE��OC�غϣ���Ҫ��n��45����n��45�������������.
��1����ODƽ����AOC
����AOD=��COD
����DOE=90��
����AOD+��EOB=90������COD+��COE=90��
����COE=��EOB
��OEҲƽ����BOC��
��2����OC��AB����DOE=90��
����AOD+��COD=90������COD+��COE=90��
���AOD=��COE
������DOB�����Ľ�Ϊ��AOD����COE��
��3������n��45������DOB![]() ��COE=��180��-n��-��45��-n��=180��-n-45��+n=135����
��COE=��180��-n��-��45��-n��=180��-n-45��+n=135����
����n��45������DOB![]() ��COE=��180��-n��-��n-45����=180��-n-n+45��=225��
��COE=��180��-n��-��n-45����=180��-n-n+45��=225��![]() 2n.
2n.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���߱���������ͼ��ʾ��7������˳���0��6��ţ���Ϊ�߸����ӣ�һö���ӷ���0����������ʱ���ƶ���ö���ӣ���һ���ƶ�1�ڶ����ƶ�2������n���ƶ�n����ͣ�����ӵĸ��ӵı����_____��
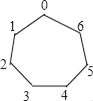
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Բ�Ľǡ�AOB=120�㣬��AB=2 ![]() cm.
cm.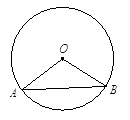
��1�����O�İ뾶r��
��2�����ӻ� ![]() �ij����������
�ij���������� ![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ĸ�BD��CE�ཻ�ڵ�O��OD=OE��AO���ӳ��߽�BC�ڵ�M�������ͼ���ҳ�����ȫ�ȵ�ֱ�������Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ, ��ABC�ڽ��ڡ�O, AD��BC��D, AE�ǡ�O��ֱ��. ��AB=6, AC=8, AE=11, ��AD�ij�.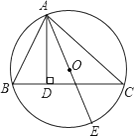
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�У� AO����BAC�Ľ�ƽ���ߣ� DΪ AO��һ�㣬�� CDΪһ������ CD�·����ȱ���CDE������BE��
��1����֤����ACD�ա�BCE��
��2���ӳ�BE��Q�� PΪBQ��һ�㣬���� CP��CQʹ CP=CQ=5���� BC=6����PQ�ij���
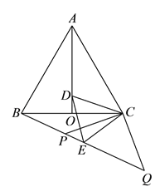
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������6�����Ϸֱ�д������1��2��3��4��5��6��С�����壬����������������д����������֮��Ϊ7����������ͬ�ļ������Ӱ�����Ӵ����������ϵ����ֵĻ�Ϊ6�ڳ�һ�������壬��������������ͼ��ͼ��ʾ����֪ͼ������ע���Dz������ϵ����֣�����*�������������ǣ� ��
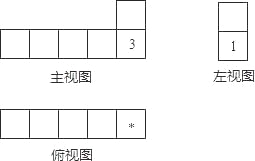
A. 2 B. 4 C. 5 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶��2��ֱ��l���O�ཻ��A��B���㣬M��N�ǡ�O�ϵ��������㣬����ֱ��l����࣬����AMB=45�㣬���ı���MANB��������ֵ�ǣ� �� 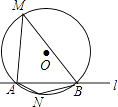
A.2 ![]()
B.4
C.4 ![]()
D.8 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ�ְ�װ�еı���չ��ͼ������Χ�����ɵõ�һ���������ģ�ͣ�
��1�����������ģ�͵�������
��2����ͼ2�Ǹ���a��b��h��ȡֵ�����ļ����������ͼ����ͼ��ͼ��ʵ�߱�ʾ�ij����Σ������������л����ü����������ͼ��
��3����h=a+b����a��b���� ![]() a2+b2��a��6b+10=0����ü�����ı������
a2+b2��a��6b+10=0����ü�����ı������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com