
【题目】如图,△ABC的高BD与CE相交于点O,OD=OE,AO的延长线交BC于点M,请你从图中找出几对全等的直角三角形,并说明理由.

【答案】△ADO≌△AEO,△DOC≌△EOB,△COF≌△BOF,△ACF≌△ABF,△ADB≌△AEC,△BCE≌△CBD.理由见解析.
【解析】
试题△ADO≌△AEO,△DOC≌△EOB,△COF≌△BOF,△ACF≌△ABF,△ADB≌△AEC,△BCE≌△CBD,利用全等三角形的判定可证明,做题时,要结合已知条件与三角形全等的判定方法逐个验证.
试题解析:△ADO≌△AEO,△DOC≌△EOB,△COF≌△BOF,△ACF≌△ABF,△ADB≌△AEC,△BCE≌△CBD.
理由如下:
在△ADO与△AEO中,∠ADO=∠AEO=90°,
![]() ,
,
∴△ADO≌△AEO(HL),
∴∠DAO=∠EAO,AD=AE,
在△DOC与△EOB中,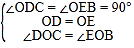 ,
,
∴△DOC≌△EOB(ASA),
∴DC=EB,OC=OB,
∴DC+AD=EB+AE,即AC=AB,
∵∠DAO=∠EAO,
∴AM⊥BC,CM=BM,
在△COF与△BOF中,∠OMC=∠OMB=90°,
![]() ,
,
∴△COF≌△BOF(HL),
在△ACF与△ABF中,∠AFC=∠AFB=90°,
![]() ,
,
∴△ACF≌△ABF(HL),
在△ADB与△AEC中,
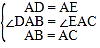 ,
,
∴△ADB≌△AEC(SAS),
在△BCE与△CBD中,∠BEC=∠CDB=90°,
![]() ,
,
∴△BCE≌△CBD(HL).


科目:初中数学 来源: 题型:
【题目】如图,∠ABE=∠ACD=Rt∠,AE=AD,∠ABC=∠ACB.求证:∠BAE=∠CAD.
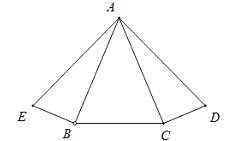
请补全证明过程,并在括号里写上理由.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= ( )
在Rt△ABE和Rt△ACD中,
∵ =AC, =AD
∴Rt△ABE≌Rt△ACD( )
∴∠BAE=∠CAD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 在平面直角坐标系中,且
在平面直角坐标系中,且![]() 、
、![]() 、
、![]() .将其平移后得到
.将其平移后得到![]() ,若
,若![]() 的对应点是
的对应点是![]() ,
,![]() ,
,![]() 的对应点
的对应点![]() 的坐标是
的坐标是![]() .
.
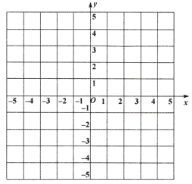
(1)在平面直角坐标系中画出![]() 和
和![]() ;
;
(2)此次平移也可看作![]() 向_________平移________个单位长度,再向__________平移了________个单位长度得到
向_________平移________个单位长度,再向__________平移了________个单位长度得到![]() ;
;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.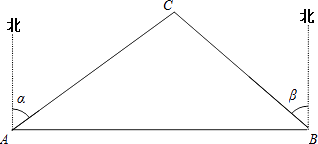
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探索:
已知点O为直线AB上一点,作射线OC,将直角三角板ODE放置在直线上方(如图①),使直角顶点与点O重合,一条直角边OD重叠在射线OA上,将三角板绕点O旋转

(1)当三角板旋转到如图②的位置时,若OD平分∠AOC,试说明OE也平分∠BOC.
(2)若OC⊥AB,垂足为点O(如图③),请直接写出与∠DOB互补的角
(3)若∠AOC=135°(如图④),三角板绕点O按顺时针从如图①的位置开始旋转,到OE边与射线OB重合结束. 请通过操作,探索:在旋转过程中,∠DOB![]() ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示. 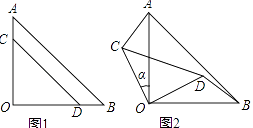
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值. 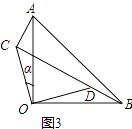
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.
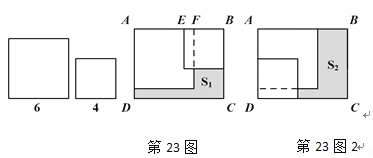
(1)在图1中,EF= ,BF= ;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的s1,s2,若m-n=2,请问S2-S1的值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com