
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示. 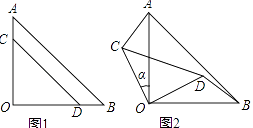
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值. 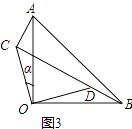
【答案】
(1)证明:如图2中,延长BD交OA于G,交AC于E.
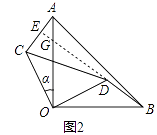
∵∠AOB=∠COD=90°,
∴∠AOC=∠DOB,
在△AOC和△BOD中,
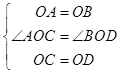 ,
,
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
∵∠DBO+∠GOB=90°,
∵∠OGB=∠AGE,
∴∠CAO+∠AGE=90°,
∴∠AEG=90°,
∴BD⊥AC.
(2)解:如图3中,设AC=x,
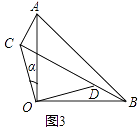
∵BD、CD在同一直线上,BD⊥AC,
∴△ABC是直角三角形,
∴AC2+BC2=AB2,
∴x2+(x+17)2=252,
解得x=7,
∵∠ODC=∠α+∠DBO=45°,∠ABC+∠DBO=45°,
∴∠α=∠ABC,
∴sinα=sin∠ABC= ![]() =
= ![]()
【解析】(1)如图2中,延长BD交OA于G,交AC于E,只要证明△AOC≌△BOD即可解决问题.(2)如图3中,设AC=x,在RT△ABC中,利用勾股定理求出x,再根据sinα=sin∠ABC= ![]() 即可解决问题.
即可解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】学生在操场上利用三角函数测量旗杆AB的高,直线l为水平地面,两个同学把30°的三角板和量角器按如图所示的方式垂直放在地面上,量角器的零刻度线与地面重合,此时旗杆顶部B的影子恰好落在三角形板的顶点D处和量角器37°的刻度C处,已知三角形板的边DE=60厘米,量角器的半径r=25厘米,量角器的圆心O到A的距离为5米. 
(1)则∠AOC=°(直接写出答案)
(2)求旗杆AB的高度(精确到0.1米,参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
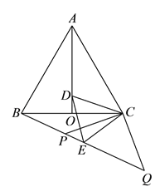
【题目】如图,等边△ABC中, AO是∠BAC的角平分线, D为 AO上一点,以 CD为一边且在 CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE.
(2)延长BE至Q, P为BQ上一点,连接 CP、CQ使 CP=CQ=5,若 BC=6,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是6个面上分别写有数字1,2,3,4,5,6的小立方体,它任意两对面上所写的两个数字之和为7.将这样相同的几个骰子按照相接触的两个面上的数字的积为6摆成一个几何体,这个几何体的三视图如图所示.已知图中所标注的是部分面上的数字,则“*”所代表的数是( )
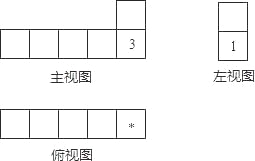
A. 2 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读句画图:如图,直线CD与直线AB相交于C,
根据下列语句画图:
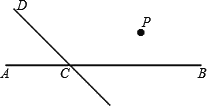
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( ) 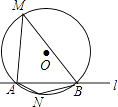
A.2 ![]()
B.4
C.4 ![]()
D.8 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 是否平行?为什么?
是否平行?为什么?
对于上述问题,小红给出了解答过程,请你在以下解答过程的括号内填上适当的内容
解:![]()
理由如下:
![]() ,
,
![]() .
.
∵四边形![]() 的内角和为360°,
的内角和为360°,
∴( ① )+( ② )=180°,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
![]() .
.
![]() .
.
又![]() , ( ③ )
, ( ③ )
![]() ,
,
![]() . ( ④ )
. ( ④ )
![]() .( ⑤ )
.( ⑤ )
查看答案和解析>>
科目:初中数学 来源: 题型:
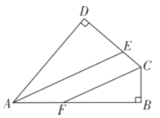
【题目】已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为8,tan∠C= ![]() ,求线段AB的长,sin∠ADB的值.
,求线段AB的长,sin∠ADB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com