
【题目】如图,圆心角∠AOB=120°,弦AB=2 ![]() cm.
cm.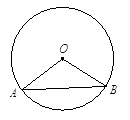
(1)求⊙O的半径r;
(2)求劣弧 ![]() 的长(结果保留
的长(结果保留 ![]() ).
).
【答案】
(1)解:作OC⊥AB于C,则AC= ![]() AB=
AB= ![]() cm.
cm.
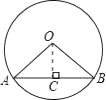
∵∠AOB=120°,OA=OB∴∠A=30°.
∴在Rt△AOC中,r=OA= ![]() =2cm
=2cm
(2)解:劣弧AB的长= ![]() πr=
πr= ![]() πcm
πcm
【解析】(1)根据垂径定理求出AC的值,由∠AOB的值,求出∠A的度数,根据三角函数求出⊙O的半径r;(2)根据弧长公式l=![]() πr,求出劣弧AB的长.
πr,求出劣弧AB的长.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对弧长计算公式的理解,了解若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.


科目:初中数学 来源: 题型:
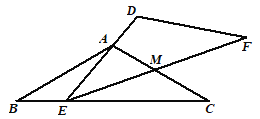
【题目】如图,![]() 和
和![]() 是两个全等的三角形,
是两个全等的三角形,![]() ,
,![]() .现将
.现将![]() 和
和![]() 按如图所示的方式叠放在一起,
按如图所示的方式叠放在一起,![]() 保持不动,
保持不动,![]() 运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
(1)求证:∠BAE=∠MEC;
(2)当E在BC中点时,请求出ME:MF的值;
(3)在![]() 的运动过程中,
的运动过程中,![]() 能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场二楼摆出一台游戏装置如图所示,小球从最上方入口处投入,每次遇到黑色障碍物,等可能地向左或向右边落下.
(1)若乐乐投入一个小球,则小球落入B区域的概率为 .
(2)若乐乐先后投两个小球,求两个小球同时落在A区域的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 在平面直角坐标系中,且
在平面直角坐标系中,且![]() 、
、![]() 、
、![]() .将其平移后得到
.将其平移后得到![]() ,若
,若![]() 的对应点是
的对应点是![]() ,
,![]() ,
,![]() 的对应点
的对应点![]() 的坐标是
的坐标是![]() .
.
(1)在平面直角坐标系中画出![]() 和
和![]() ;
;
(2)此次平移也可看作![]() 向_________平移________个单位长度,再向__________平移了________个单位长度得到
向_________平移________个单位长度,再向__________平移了________个单位长度得到![]() ;
;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,对角线AC、BD相交于点O.
,对角线AC、BD相交于点O.
⑴若AB=BC,则![]() 是_______.
是_______.
⑵若AC=BD,则![]() 是_________.
是_________.
⑶若∠BCD=90°,则![]() 是_________.
是_________.
⑷若OA=OB,且OA⊥OB,则![]() 是_________.
是_________.
⑸若AB=BC,且AC=BD,则![]() 是_________.
是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探索:
已知点O为直线AB上一点,作射线OC,将直角三角板ODE放置在直线上方(如图①),使直角顶点与点O重合,一条直角边OD重叠在射线OA上,将三角板绕点O旋转

(1)当三角板旋转到如图②的位置时,若OD平分∠AOC,试说明OE也平分∠BOC.
(2)若OC⊥AB,垂足为点O(如图③),请直接写出与∠DOB互补的角
(3)若∠AOC=135°(如图④),三角板绕点O按顺时针从如图①的位置开始旋转,到OE边与射线OB重合结束. 请通过操作,探索:在旋转过程中,∠DOB![]() ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB. 
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com