
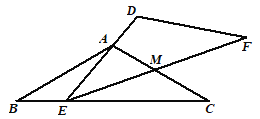
【题目】如图,![]() 和
和![]() 是两个全等的三角形,
是两个全等的三角形,![]() ,
,![]() .现将
.现将![]() 和
和![]() 按如图所示的方式叠放在一起,
按如图所示的方式叠放在一起,![]() 保持不动,
保持不动,![]() 运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
(1)求证:∠BAE=∠MEC;
(2)当E在BC中点时,请求出ME:MF的值;
(3)在![]() 的运动过程中,
的运动过程中,![]() 能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
【答案】(1)证明见解析;(2)见解析;(3)见解析.
【解析】
(1)已知△ABC≌△DEF,根据全等三角形的性质可得∠ABC=∠DEF,又因∠AEC=∠B+∠BAE,∠AEC=∠AEM+∠MEC,即可得∠B+∠BAE=∠AEM+∠MEC,所以∠BAE=∠MEC;(2)当E为BC中点时, AB=AC,根据等腰三角形三线合一的性质可得AE⊥BC,∠EAM=60°,再由∠DEM=30°即可证得AC⊥EF; 在Rt△ABE中,∠B=30°,![]() ,求得BE=
,求得BE=![]() ,即可求得BC=3;在Rt△CEM中,∠C=30°,EC=
,即可求得BC=3;在Rt△CEM中,∠C=30°,EC=![]() E,求得EM=
E,求得EM=![]() ,根据全等三角形的性质可得BC=EF=3,所以FM= EF-EM=
,根据全等三角形的性质可得BC=EF=3,所以FM= EF-EM=![]() ,即可得EM:FM=1:3 ;(3)分AM=AE、EA=EM、
,即可得EM:FM=1:3 ;(3)分AM=AE、EA=EM、![]() 三种情况求解即可.
三种情况求解即可.
(1)证明:∵△ABC≌△DEF
∴∠ABC=∠DEF
∵∠AEC=∠B+∠BAE,∠AEC=∠AEM+∠MEC;
∴∠B+∠BAE=∠AEM+∠MEC,
即∠BAE=∠MEC ;
(2)当E为BC中点时,
∵AB=AC,
∴AE⊥BC,BE=EC=![]() ,∠EAM=60°,
,∠EAM=60°,
又∵∠DEM=30°,
∴AC⊥EF;
∵![]() ,
,![]() ,
,
∴∠B=∠C=30°,
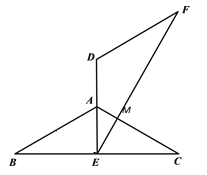
在Rt△ABE中,∠B=30°,![]() ,
,
∴BE=![]() ,
,
∴BC=3;
在Rt△CEM中,∠C=30°,EC=![]() ,
,
∴EM=![]() ,
,
∵△ABC≌△DEF,
∴BC=EF=3,
∴FM= EF-EM=![]() ,
,
∴EM:FM=1:3;
(3)当![]() 或2时,
或2时,![]() 是等腰三角形.
是等腰三角形.
①当![]() 时,如图,
时,如图,

![]()
![]() ,
,
此时点E与点B重合,与题意矛盾(舍去 ) ;
②当![]() 时,如图,
时,如图,

由(1)知,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
③当![]() 时,如图,
时,如图,

则![]() ,
,
![]() ,
,
取BE中点I,连结AI,
则![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
设![]() ,在
,在![]() 中,
中,
由勾股定理,得![]() ,
,
即![]() ,解得
,解得![]()
![]() .
.
综上所述,当![]() 或2时,
或2时,![]() 是等腰三角形.
是等腰三角形.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】操作与探究
图(1)
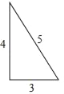
定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小东用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分用24根火柴棒摆出直角“整数三角形”;
小军受到小东、小颖的启发,用30根火柴棒摆出直角“整数三角形”;
(1)请你画出小颖和小军摆出的直角“整数三角形”的示意图;
(2)你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
①摆出一个等腰“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,小芳和小亮去商店购买学习用品,小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍,已知每支钢笔的价格比每本笔记本的价格少2元.
(1)求每支钢笔和每本笔记本各是多少元;
(2)学校运动会后,班主任拿出200元学校奖励基金交给小芳,再次购买上述价格的钢笔和笔记本共48件作为奖品,奖励给校运动会中表现突出的同学,经双方协商,商店给出优惠是购买商品的总金额超出50的部分给打九折,请问小芳至少要买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0),与y轴相交于点C(0,3).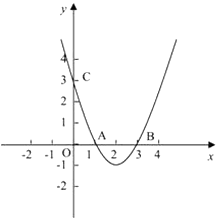
(1)求抛物线的函数关系式.
(2)将y=ax2+bx+c化成y=a(x﹣m)2+k的形式(请直接写出答案).
(3)若点D(3.5,m)是抛物线y=ax2+bx+c上的一点,请求出m的值,并求出此时△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,∠B=∠C,要使四边形ABCD为矩形,还需添加一个条件,这个条件可以是( )
A. AB=CD
B. AC=BD
C. ∠A=∠D
D. ∠A=∠B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图1,先把正方形ABCD对折,折痕为MN.
第二步:点G在线段 MD上,将△GCD沿GC翻折,点D恰好落在MN上,记为点P,连接BP.
(1)判断△PBC的形状,并说明理由;
(2)作点C关于直线AP的对称点C′,连接PC′、DC′.
①在图2中补全图形,并求出∠APC′的度数;
②猜想∠PC′D的度数,并加以证明;(温馨提示:当你遇到困难时,不妨连接AC′、CC′,研究图形中特殊的三角形)
查看答案和解析>>
科目:初中数学 来源: 题型:
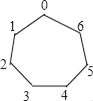
【题目】一个七边形棋盘如图所示,7个顶点顺序从0到6编号,称为七个格子.一枚棋子放在0格,现在依逆时针移动这枚棋子,第一次移动1格,第二次移动2格,…,第n次移动n格.则不停留棋子的格子的编号有_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com