
����Ŀ��ȡһ�������ε�ֽƬ�����۵�����������������£�
��һ������ͼ1���Ȱ�������ABCD���ۣ��ۺ�ΪMN��
�ڶ�������G���߶� MD�ϣ�����GCD��GC���ۣ���Dǡ������MN�ϣ���Ϊ��P������BP��
��1���жϡ�PBC����״����˵�����ɣ�
��2������C����ֱ��AP�ĶԳƵ�C�䣬����PC�䡢DC�䣮
����ͼ2�в�ȫͼ�Σ��������APC��Ķ�����
�ڲ����PC��D�Ķ�����������֤��������ܰ��ʾ��������������ʱ����������AC�䡢CC�䣬�о�ͼ��������������Σ�
���𰸡�
��1���⣺��PBC�ǵȱ������Σ��������£�
���ı���ABCD�������Σ�
��AB=BC=CD����ABC=90�㣬
���۵������ʵã�BN=NC= ![]() BC=
BC= ![]() PC��MN��BC��
PC��MN��BC��
��PB=PC����PNC=90�㣬
��Rt��PNC��sin��NPC= ![]() =
= ![]() ��
��
���NPC=30�㣬
���PCB=60�㣬
���PBC�ǵȱ�������
��2���⣺�ٲ�ȫͼ����ͼ2��ʾ��
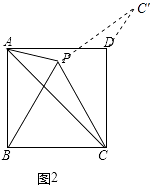
�ɢٵã���PCB=��PBC=��BPC=60�㣬PB=PC=BC��
�ߡ�ABC=90�㣬
���ABP=90�㩁60��=30�㣬
��AB=BC��
��AB=PB��
���BAP=��BPA= ![]() ��180�㩁30�㣩=75�㣬
��180�㩁30�㣩=75�㣬
���APC=��BPA+��BPC=75��+60��=135�㣬
��C����ֱ��AP�ĶԳƵ�ΪC�䣬
���APC'=��APC=135�㣻
������AC'��CC'����ͼ3��ʾ��
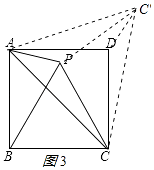
�ɶԳƵ����ʵã�AC=AC'����CAP=��C'AP=30�㣬
���CAC'=60�㣬
���CAC'�ǵȱ������Σ�
��AC'=CC'����AC'C=60�㣬
�ڡ�AC'D�͡�CC'D�У� 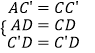 ��
��
���AC'D�ա�CC'D��SSS����
���AC'D=��CC'D= ![]() ��AC'C=30�㣬
��AC'C=30�㣬
�ߡ�AC'P=��ACP=15�㣬
���PC'D=15�㣮
����������1���������ε����ʵó�AB=BC=CD����ABC=90�㣬���۵������ʵã�BN=NC= ![]() BC=
BC= ![]() PC��MN��BC���ó�PB=PC����PNC=90�㣬��Rt��PNC�У������Ǻ����ó�sin��NPC=
PC��MN��BC���ó�PB=PC����PNC=90�㣬��Rt��PNC�У������Ǻ����ó�sin��NPC= ![]() =
= ![]() �������NPC=30�㣬�ó���PCB=60�㣬���ɵó����ۣ���2���ٸ������ⲹȫͼ�Σ��ɢٵã���PCB=��PBC=��BPC=60�㣬PB=PC=BC���ɵ��������ε����ʺ��������ڽǺͶ����ó���BAP=��BPA=75�㣬�����APC=��BPA+��BPC=135�㣬���ɵó������ʵó���APC'=��APC=135�㣻���ɶԳƵ����ʵã�AC=AC'����CAP=��C'AP=30�㣬֤����CAC'�ǵȱ������Σ��ó�AC'=CC'����AC'C=60�㣬��SSS֤����AC'D�ա�CC'D���ó���AC'D=��CC'D=
�������NPC=30�㣬�ó���PCB=60�㣬���ɵó����ۣ���2���ٸ������ⲹȫͼ�Σ��ɢٵã���PCB=��PBC=��BPC=60�㣬PB=PC=BC���ɵ��������ε����ʺ��������ڽǺͶ����ó���BAP=��BPA=75�㣬�����APC=��BPA+��BPC=135�㣬���ɵó������ʵó���APC'=��APC=135�㣻���ɶԳƵ����ʵã�AC=AC'����CAP=��C'AP=30�㣬֤����CAC'�ǵȱ������Σ��ó�AC'=CC'����AC'C=60�㣬��SSS֤����AC'D�ա�CC'D���ó���AC'D=��CC'D= ![]() ��AC'C=30�㣬�ɡ�AC'P=��ACP=15�㣬���ɵó���PC'D=15�㣮
��AC'C=30�㣬�ɡ�AC'P=��ACP=15�㣬���ɵó���PC'D=15�㣮
�����㾫����������Ҫ������ȫ�������ε����ʺ������ε����ʵ����֪ʶ�㣬��Ҫ����ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ��������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������β�����ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��CD��ֱ��EF���أ����Ҫ����������ʹ��MQ��NP����ô�������������ж�MQ��NP����( )
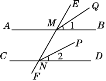
A. ��1����2 B. ��BMF����DNF
C. ��AMQ����CNP D. ��1����2����BMF����DNF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����CED��Ϊ�ȱ������Σ���B��C��D���㹲�ߣ��߶�BE��AD�ཻ�ڵ�O��AF��BE�ڵ�F����OF=1����AF�ij�Ϊ��������
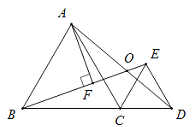
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ������ȫ�ȵ������Σ�
������ȫ�ȵ������Σ�![]() ��
��![]() .�ֽ�
.�ֽ�![]() ��
��![]() ����ͼ��ʾ�ķ�ʽ������һ����
����ͼ��ʾ�ķ�ʽ������һ����![]() ���ֲ�����
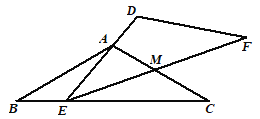
���ֲ�����![]() �˶��������㣺��E�ڱ�BC���˶�(�����B��C�غ�)���ұ�DEʼ�վ�����A��EF��AC���ڵ�M .
�˶��������㣺��E�ڱ�BC���˶�(�����B��C�غ�)���ұ�DEʼ�վ�����A��EF��AC���ڵ�M .
��1����֤����BAE=��MEC��
��2����E��BC�е�ʱ�������ME��MF��ֵ��
��3����![]() ���˶������У�
���˶������У�![]() �ܷɵ��������Σ����ܣ���ֱ��д�����з���������BE�ij��������ܣ�����˵��������
�ܷɵ��������Σ����ܣ���ֱ��д�����з���������BE�ij��������ܣ�����˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����Ӧ����Сѧ��ÿ�����1Сʱ���ĺ��٣�ijУ��չ����ʽ�����ġ��������������С����ij��ͬѧ�μӶ�������������˵�����ͳ�ƣ��������������ͼ1��ͼ2���������ͼ1��ͼ2�����⣬�ش��������⣺
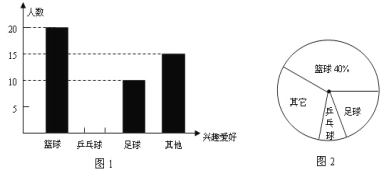
��1��С�����������༶�ж�����ѧ�����μ����������ѧ��������ռ�İٷֱ��Ƕ��٣�
��2�����㽫ͼ1�С�ƹ�����ֲ���������
��3���������ͳ��ͼ�б�ʾ���������ε�Բ�ĽǵĶ�����
��4�������ѧУ����1200��ѧ�������Ʋμ�ƹ������ѧ���ж�����ѧ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABE=��ACD=Rt����AE=AD����ABC=��ACB.��֤����BAE=��CAD��
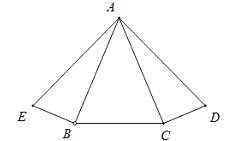
�벹ȫ֤�����̣�����������д�����ɣ�
֤��������ABC�У�
�ߡ�ABC=��ACB
��AB= �� ��
��Rt��ABE��Rt��ACD��
�� =AC�� =AD
��Rt��ABE��Rt��ACD�� ��
���BAE=��CAD�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OPƽ�֡�AOB����AOP=15�㣬PC��OA��PD��OA�ڵ�D��PC=4����PD�ij�Ϊ(����)

A. 2 B. 3 C. 4 D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���¥�ڳ�һ̨��Ϸװ����ͼ��ʾ��С������Ϸ���ڴ�Ͷ�룬ÿ��������ɫ�ϰ���ȿ��ܵ���������ұ����£�
��1��������Ͷ��һ��С����С������B����ĸ���Ϊ ��
��2���������Ⱥ�Ͷ����С��������С��ͬʱ����A����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���۵�����ABCD��һ��AD��ʹ��D����BC�ߵĵ�F������֪�ۺ�AE=5 ![]() cm����tan��EFC=
cm����tan��EFC= ![]() �������ABCD���ܳ��� ��
�������ABCD���ܳ��� �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com