
【题目】为了响应“中小学生每天锻炼1小时”的号召,某校开展了形式多样的“阳光体育”活动,小明对某班同学参加锻炼的情况进行了调查与统计,并绘制了下面的图1与图2.根据你对图1与图2的理解,回答下列问题:
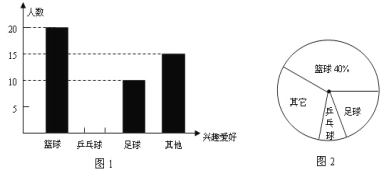
(1)小明调查的这个班级有多少名学生,参加足球锻炼的学生人数所占的百分比是多少?
(2)请你将图1中“乒乓球”部分补充完整.
(3)求出扇形统计图中表示“足球”的扇形的圆心角的度数.
(4)若这个学校共有1200名学生,估计参加乒乓球活动的学生有多少名学生?
【答案】(1)小明调查的这个班级有50名学生,参加足球锻炼的学生人数所占的百分比是20%;(2)见解析;(3)扇形统计图中表示“足球”的扇形的圆心角的度数为72°;(4)参加乒乓球活动的学生有120名学生
【解析】
(1)利用参加篮球锻炼的学生人数除以其所占该班总人数的百分比即可求出该班总人数,然后利用参加足球锻炼的学生人数除以该班总人数即可求出所占的百分比;
(2)利用该班总人数减去“篮球”、“足球”和“其它”的人数即可求出“乒乓球”的人数,然后补全条形统计图即可;
(3)利用参加足球锻炼的学生人数所占的百分比再乘360°即可求出结论;
(4)求出参加乒乓球活动的学生所占的百分比再乘1200即可求出结论.
解:(1)该班总人数为20÷40%=50(名)
参加足球锻炼的学生人数所占的百分比是10÷50×100%=20%
答:小明调查的这个班级有50名学生,参加足球锻炼的学生人数所占的百分比是20%.
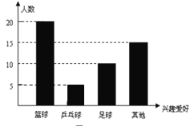
(2)“乒乓球”的人数为50-20-10-15=5(名)
补全条形统计图如下
(3)表示“足球”的扇形的圆心角的度数为20%×360°=72°
答:扇形统计图中表示“足球”的扇形的圆心角的度数为72°.
(4)5÷50×1200=120(名)
答:参加乒乓球活动的学生有120名学生.


科目:初中数学 来源: 题型:
【题目】下列命题中,不正确的是( )
A.垂直平分弦的直线经过圆心
B.平分弦的直径一定垂直于弦
C.平行弦所夹的两条弧相等
D.垂直于弦的直径必平分弦所对的弧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD交于点O,AC⊥BC,且ABCD的周长为36,△OCD的周长比△OBC的周长大2.
(1)求BC,CD的长;
(2)求ABCD的面积.
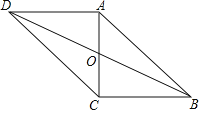
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,∠B=∠C,要使四边形ABCD为矩形,还需添加一个条件,这个条件可以是( )
A. AB=CD
B. AC=BD
C. ∠A=∠D
D. ∠A=∠B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8中图①,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向
右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图1,先把正方形ABCD对折,折痕为MN.
第二步:点G在线段 MD上,将△GCD沿GC翻折,点D恰好落在MN上,记为点P,连接BP.
(1)判断△PBC的形状,并说明理由;
(2)作点C关于直线AP的对称点C′,连接PC′、DC′.
①在图2中补全图形,并求出∠APC′的度数;
②猜想∠PC′D的度数,并加以证明;(温馨提示:当你遇到困难时,不妨连接AC′、CC′,研究图形中特殊的三角形)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①同位角相等;
②若∠A+∠B+∠C=180°,则∠A、∠B、∠C互补;
③同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交;
④同一平面内两条直线的位置关系可能是平行或垂直;
⑤有公共顶点并且相等的角是对顶角.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,BC=4,点M、N分别在边AD和BC上,沿MN折叠四边形ABCD,使点A、B分别落在A1、B1处,得四边形A1B1NM,其中点B1在DC上,过点M作ME⊥BC于点E,连接BB1 , 给出下列结论:①∠MNB1=∠ABB1;②△MEN∽△BCB1;③ ![]() 的值为定值;④当B1C=
的值为定值;④当B1C= ![]() DC时,AM=
DC时,AM= ![]() ,其中正确结论的序号是 . (把所有正确结论的序号都在填在横线上)
,其中正确结论的序号是 . (把所有正确结论的序号都在填在横线上) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点A、B、C都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形,试在方格纸上按下列要求画格点三角形:
(1)将△ABC先向下平移4个单位,再向右平移2个单位得到△A1B1C1;
(2)线段AC与A1C1的关系 ;
(3)画AC边上的高线BE;(利用网格点和直尺画图)
(4)连接CC1,则∠BCC1= °.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com