
【题目】下列命题中,不正确的是( )
A.垂直平分弦的直线经过圆心
B.平分弦的直径一定垂直于弦
C.平行弦所夹的两条弧相等
D.垂直于弦的直径必平分弦所对的弧
【答案】B
【解析】A. 根据垂径定理的推论可知,垂直平分弦的直线经过圆心;A不符合题意。
B. 直径是最长的弦,任意两条直径互相平分,但不一定互相垂直,故被平分飞弦不能是直径;B符合题意。
C. 如图所示,
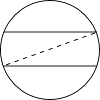
两弦平行,则圆周角相等,圆周角相等,则弧相等;C不符合题意。
D. 根据垂径定理可知,垂直于弦的直径必平分弦所对的弧;D不符合题意。
所以答案是:B.
【考点精析】利用垂径定理和圆心角、弧、弦的关系对题目进行判断即可得到答案,需要熟知垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
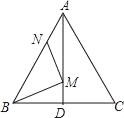
【题目】如图,在等边△ABC中,AB=6,N为AB上一点,且AN=2,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM,MN,则BM+MN的最小值是( )
A. 8 B. 10 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
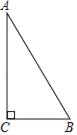
【题目】如图,在Rt△ABC中,∠C=90°,AC=4.
(1)若BC=2,求AB的长;
(2)若BC=a,AB=c,求代数式(c﹣2)2﹣(a+4)2+4(c+2a+3)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
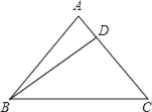
【题目】已知等腰三角形ABC的底边长BC=20cm,D是AC上的一点,且BD=16cm,CD=12cm.
(1)求证:BD⊥AC;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为菱形ABCD的BC边的中点,动点F在对角线AC上运动,连接BF、EF,设AF=x,△BEF的周长为y,那么能表示y与x的函数关系的大致图象是( )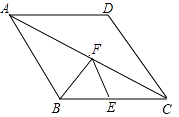
A.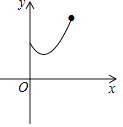
B.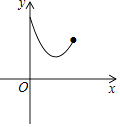
C.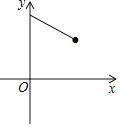
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB,CD被直线EF所截,如果要添加条件,使得MQ∥NP,那么下列条件中能判定MQ∥NP的是( )
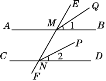
A. ∠1=∠2 B. ∠BMF=∠DNF
C. ∠AMQ=∠CNP D. ∠1=∠2,∠BMF=∠DNF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x-1)2-4,AB为半圆的直径,求这个“果圆”被y轴截得的弦CD的长 . 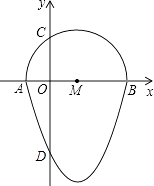
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() (x≠0)的图象上.
(x≠0)的图象上.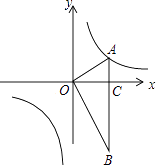
(1)求反比例函数y= ![]() (x≠0)的解析式和点B的坐标;
(x≠0)的解析式和点B的坐标;
(2)若将△BOA绕点B按逆时针方向旋转60°得到△BDE(点O与点D是对应点),补全图形,直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“中小学生每天锻炼1小时”的号召,某校开展了形式多样的“阳光体育”活动,小明对某班同学参加锻炼的情况进行了调查与统计,并绘制了下面的图1与图2.根据你对图1与图2的理解,回答下列问题:
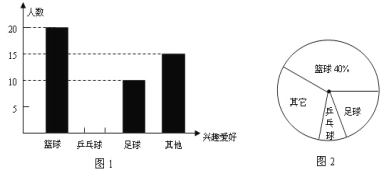
(1)小明调查的这个班级有多少名学生,参加足球锻炼的学生人数所占的百分比是多少?
(2)请你将图1中“乒乓球”部分补充完整.
(3)求出扇形统计图中表示“足球”的扇形的圆心角的度数.
(4)若这个学校共有1200名学生,估计参加乒乓球活动的学生有多少名学生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com