
【题目】操作与探究
图(1)
定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
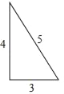
小东用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分用24根火柴棒摆出直角“整数三角形”;
小军受到小东、小颖的启发,用30根火柴棒摆出直角“整数三角形”;
(1)请你画出小颖和小军摆出的直角“整数三角形”的示意图;
(2)你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
①摆出一个等腰“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
【答案】(1)小颖摆出直角“整数三角形”三边为6,8,10;小军摆出的直角“整数三角形”三边为5,12,13.(2)①详见解析;②详见解析.
【解析】
(1)利用勾股定理求出6,8,10和5,12,13符合要求,即可得出答案;
(2)要摆出等腰“整数三角形”,需保证三边长和面积都是整数,由三线合一可知,等腰三角形的一半是直角三角形,即画出直角三角形后再补充完整的等腰三角形;
(3)摆出一个非特殊“整数三角形”:要摆出“整数三角形”,需使三角形的底与高均为整数,可将两个直角三角形进行组合,常见的等高直角三角形有:6、8、10与8、15、17;9、12、15与5、12、13.
(1)如图1,
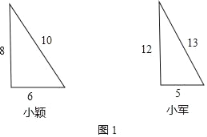
小颖摆出直角“整数三角形”三边为6,8,10;
小军摆出的直角“整数三角形”三边为5,12,13.
(2)摆出如图2所示三个不同的等腰“整数三角形”:
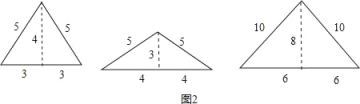
(3)摆出如图3所示一个非特殊“整数三角形”:


科目:初中数学 来源: 题型:
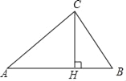
【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校有一块三角形草坪,数学课外小组的同学测得其三边的长分别为AB=200米,AC=160米,BC=120米.
(1)小明根据测量的数据,猜想△ABC是直角三角形,请判断他的猜想是否正确,并说明理由;
(2)若计划修一条从点C到BA边的小路CH,使CH⊥AB于点H,求小路CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
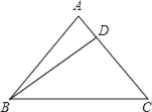
【题目】已知等腰三角形ABC的底边长BC=20cm,D是AC上的一点,且BD=16cm,CD=12cm.
(1)求证:BD⊥AC;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BDC=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.
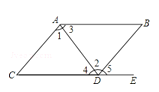
A.1B.2C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB,CD被直线EF所截,如果要添加条件,使得MQ∥NP,那么下列条件中能判定MQ∥NP的是( )
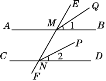
A. ∠1=∠2 B. ∠BMF=∠DNF
C. ∠AMQ=∠CNP D. ∠1=∠2,∠BMF=∠DNF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.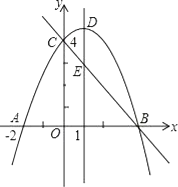
(1)求抛物线的解析式;
(2)若直线BC的函数解析式为y’=kx+b,求当满足y<y’时,自变量x的取值范围.
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 是两个全等的三角形,
是两个全等的三角形,![]() ,
,![]() .现将
.现将![]() 和
和![]() 按如图所示的方式叠放在一起,
按如图所示的方式叠放在一起,![]() 保持不动,
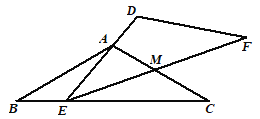
保持不动,![]() 运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
(1)求证:∠BAE=∠MEC;
(2)当E在BC中点时,请求出ME:MF的值;
(3)在![]() 的运动过程中,
的运动过程中,![]() 能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com