
����Ŀ����ͼ��������y=ax2+bx+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A�͵�B�����е�A������Ϊ����2��0���������ߵĶԳ���x=1�������߽��ڵ�D����ֱ��BC���ڵ�E��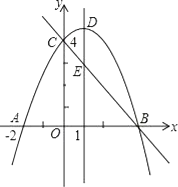
��1���������ߵĽ���ʽ��
��2����ֱ��BC�ĺ�������ʽΪy��=kx+b,������y<y��ʱ���Ա���x��ȡֵ��Χ.
��3��ƽ����DE��һ����ֱ��l��ֱ��BC�ཻ�ڵ�P�����������ཻ�ڵ�Q������D��E��P��QΪ������ı�����ƽ���ı��Σ����P�����꣮
���𰸡�
��1���⣺��������y=ax2+bx+c��a��0������C��0��4����
��c=4 �٣�
�߶Գ���x=- ![]() =1��
=1��
��b=-2a �ڣ�
�������߹���A��-2��0����
��0=4a-2b+c �ۣ�
�ɢ٢ڢ۽�ã�a=- ![]() ��b=1��c=4��
��b=1��c=4��
�������ߵĽ���ʽΪy=- ![]() x2+x+4��
x2+x+4��
��2���⣺��A����2��0�����Գ���x=1��
��B��4��0��
����ͼ��x<0 ��x>4ʱ��y
��3���⣺��֪DE��PQ����DE=PQʱ����D��E��P��QΪ������ı�����ƽ���ı��Σ�
���P�������ǣ�m����m+4�������Q�������ǣ�m���� ![]() m2+m+4����
m2+m+4����
��|��m+4+ ![]() m2��m��4|=DE=
m2��m��4|=DE= ![]() ��
��

��m=1��m=3��m= ![]() ��m=
��m= ![]()
��m=1ʱ���߶�PQ��DE�غϣ���ȥ��
��P1��3��1����
P2�� ![]() ��
�� ![]() ����
����
P3�� ![]() ��
�� ![]() ��.
��.
����������1������һ�����ݵ�C����������c=4�����ݶԳ���x=1���ó�b=-2a ������A������������ʽ�ó�0=4a-2b+c ��������⣬���������������ʽ�������������ݶ��κ����ĶԳ��ԣ��ɵ�A�����꼰�����ߵĶԳ���x=1�������B�����꣬Ȼ���躯������ʽΪ����ʽ���ٽ���C������������a��ֵ�����������������ʽ��
��2���������B�����꣬���ݵ�A��B�����꣬�۲캯��ͼ��Ҫʹy<y��ʱ����Ҫ�۲������ߵ���ֱ��BC�IJ��֣�������������
��3��ץס��֪����ƽ����DE��һ����ֱ��l����֪DE��PQ����P�͵�Q�ĺ�������ȣ�Ҫ֤��D��E��P��QΪ������ı�����ƽ���ı��Σ�ֻ��֤��DE=PQ���ɡ��ȸ��ݵ�P�͵�Q�ĺ�������ȣ��ֱ�����������꣬�ٸ���DE=PQ�������̣���⼴����õ�P�����ꡣ
�����㾫����ͨ���������ƽ���ı��ε��ж������ʣ�������һֱ�߹�ƽ���ı������Խ��ߵĽ��㣬������ֱ�߱�һ��Ա߽��µ��߶��ԶԽ��ߵĽ���Ϊ�е㣬����������ֱ�߶��ȷִ�ƽ���ı��ε���������Խ����⣮


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У���A=90�㣬AB=3��AD=4��BC=12��CD=13�����ı���ABCD�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������̽��
ͼ��1��
���壺���߳���������������������γ�Ϊ�����������Ρ���
��ѧѧϰС���ͬѧ��32���ȳ��Ļ�����ÿ�����ȼ�Ϊ1����λ����ȡ�����ɸ�����β���������������Σ�����̽�����
С����12���������ڳ���ͼ��ʾ�ġ����������Ρ���
Сӱ����24�������ڳ�ֱ�ǡ����������Ρ���
С���ܵ�С����Сӱ����������30�������ڳ�ֱ�ǡ����������Ρ���
��1�����㻭��Сӱ��С���ڳ���ֱ�ǡ����������Ρ���ʾ��ͼ��
��2�����ܷ�Ҳ����ȡ�����ɸ���������Ҫ��ڳ������������Ρ�������ܣ��뻭��ʾ��ͼ��������ܣ���˵�����ɣ�
�ٰڳ�һ�����������������Ρ���
�ڰڳ�һ�������⣨�ȷ�ֱ�������Σ�Ҳ�ǵ��������Σ������������Ρ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ʾʵ��a��b�ĵ��������ϵ�λ����ͼ��ʾ�����н��۴������( )
![]()
A. ![]() ��1��
��1��![]() B. 1����a��b C. 1��
B. 1����a��b C. 1��![]() ��b D. ��b��a����1
��b D. ��b��a����1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������A��B��C��A���������B���ٵ�C�����ٺ��У����ִ�AC���е�D������ijһ��������ֱ�ߺ��У���һ�������ʹ���֣�����ͬʱ����ͬʱ��������A��B��C�ϵ�ij��E������֪AB��BC��200�����ABC��90�������ֵ��ٶ��ǻ����ٶȵ�2����
(1)ѡ���⣺��������֮��E��( )
A�����߶�AB��
B�����߶�BC��
C���������߶�AB�ϣ�Ҳ�������߶�BC��
(2)���ִӳ��������������������˶��ٺ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ�ĸ����У� ��
�ٷ���![]() �ķǸ�������ֻ��
�ķǸ�������ֻ��![]() �����������߶���β˳����������ɵ�ͼ�ν��������Σ������
�����������߶���β˳����������ɵ�ͼ�ν��������Σ������![]() ����ô
����ô![]() ��ֱ�������Σ��ܸ��߶���ȵĶ������������Σ������һ��������ֻ��һ�����������ε��ڲ�����ô���������һ���Ƕ۽������Σ�
��ֱ�������Σ��ܸ��߶���ȵĶ������������Σ������һ��������ֻ��һ�����������ε��ڲ�����ô���������һ���Ƕ۽������Σ�
A.0��B.1��C.2��D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����С����С��ȥ�̵깺��ѧϰ��Ʒ��С����30ԪǮ����ֱʵ�������С����25ԪǮ����ʼDZ�������2������֪ÿ֧�ֱʵļ۸��ÿ���ʼDZ��ļ۸���2Ԫ��
��1����ÿ֧�ֱʺ�ÿ���ʼDZ����Ƕ���Ԫ��
��2��ѧУ�˶���������ó�200ԪѧУ��������С�����ٴι��������۸�ĸֱʺͱʼDZ���48����Ϊ��Ʒ��������У�˶����б���ͻ����ͬѧ����˫��Э�̣��̵�����Ż��ǹ�����Ʒ���ܽ���50�IJ��ָ�����ۣ�����С������Ҫ�����֧�ֱʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��x���ཻ������A��1��0����B��3��0������y���ཻ�ڵ�C��0��3����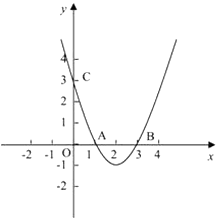
��1���������ߵĺ�����ϵʽ.
��2����y=ax2+bx+c����y=a��x��m��2+k����ʽ(��ֱ��д����).
��3������D��3.5��m����������y=ax2+bx+c�ϵ�һ�㣬�����m��ֵ���������ʱ��ABD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
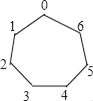
����Ŀ��һ���߱���������ͼ��ʾ��7������˳���0��6��ţ���Ϊ�߸����ӣ�һö���ӷ���0����������ʱ���ƶ���ö���ӣ���һ���ƶ�1�ڶ����ƶ�2������n���ƶ�n����ͣ�����ӵĸ��ӵı����_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com