
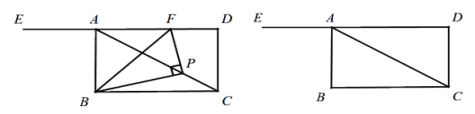
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ���P�ǶԽ���AC��һ���㣨�����C�͵�![]() �غϣ�������PB������P��
�غϣ�������PB������P��![]() ������DA�ڵ�F������BF�� ��֪AD=3
������DA�ڵ�F������BF�� ��֪AD=3![]() ��CD=3����CP�ij�Ϊx��
��CD=3����CP�ij�Ϊx��
��1���߶�![]() ����Сֵ ����x=1ʱ��
����Сֵ ����x=1ʱ��![]() ��
��
��2����ͼ��������![]() �˶���AC���е�ʱ��
�˶���AC���е�ʱ��![]() ��
��![]() �Ľ���ΪG��
�Ľ���ΪG��![]() ���е�Ϊ
���е�Ϊ![]() �����߶�GH�ij��ȣ�
�����߶�GH�ij��ȣ�
��3������![]() ���˶��Ĺ����У�
���˶��Ĺ����У�
����̽��![]() �Ƿ�ᷢ���仯�������ı䣬�����
�Ƿ�ᷢ���仯�������ı䣬�����![]() ��С�����ı䣬��˵�����ɣ�
��С�����ı䣬��˵�����ɣ�
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() �ǵ��������Σ�
�ǵ��������Σ�
���𰸡���1��![]() ��30�㣻��2��
��30�㣻��2��![]() ����3����30�㣻��x=3��3
����3����30�㣻��x=3��3![]()
��������
��1����BP��Сʱ����BP��AC���������������ε����ʣ������BPֵ����x=1ʱ���ɵó���BPN�ס�PMF���ɴ˿ɵó�tan��FBP��ֵ����ɵõ���FBP��ֵ��
��2����֤BP��ֱƽ��AP�����FP=![]() ��֤GH��Rt��FGP���ߣ���GH=
��֤GH��Rt��FGP���ߣ���GH=![]() FP��
FP��
��3���ٹ�P��PN��BC��AD��M����֤��FMP�ס�PNB����PC=x��PN=![]() �������NC��MP��BN���ȣ�tan��FBP=
�������NC��MP��BN���ȣ�tan��FBP=![]() =
=![]() =
=![]() ��������á�FBP�Ĵ�С��
��������á�FBP�Ĵ�С��
�ڷ��������������⼴��.
��1����BP��Сʱ��A��F�غϣ���BP��AC��
��AD=3![]() ��CD=3��
��CD=3��
��AC=6����BAC=30�㣬
��Rt��ABC��Rt��APB����BAC=��PAB��
���ABC�ס�APB��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��BP=![]() ��
��
��PM��BC��N����AD��M��

��x=1ʱ��PN=![]() ��MP=
��MP=![]() ��CN=
��CN=![]() ��BN=
��BN=![]() ��
��
�ߡ�BNP=��PMF=��BPM=90�㣬
���FPM+��PFM=90�㣬��FPM+��BPN=90��,
���PFM=��BPN��
���BPN�ס�PMF��
��![]() =
=![]() =
=![]() =tan��FBP=
=tan��FBP=![]() ��
��
�൱x=1ʱ����FBP=30��;
��2����PΪAC�е㣬

��AP=PC=AB=3��
���ABP=��APB=��BAP=60�㣬
��Rt��ABF��Rt��PBF��AB=BP��BF=BF��
��Rt��ABF��Rt��PBF��
��AG=PG����AGB=��PGB=90�㣬
��BF��ֱƽ��AP��
��Rt��BFP�У���PBF=30�㣬BP=3��
��PF=tan30����3=![]() ��
��
��HΪPF�е㣬
��GHΪRt��PGF�����ߣ�
��GH=![]() PF=
PF=![]() ;
;
��3���١�FBP=30�㣬
��P��PN��BC��AD��M��
�ߡ�PBN=��FPM����BPN=��PFM��
���FMP�ס�PNB��
��CP=x����PN=![]() ��NC=
��NC=![]() x��MP=3-
x��MP=3-![]() x��BN=3
x��BN=3![]() -
-![]() x��
x��
��tan��FBP=![]() =
=![]() =
=![]() ��
��
���FBP=30�㣻
�ڣ�i����AF=FP�����FPA=��FAP=30�㣬
��AB=BP���ҡ�ABPΪ�ȱ������Σ�
��BFΪ��ABP��ֱƽ���ߣ�
��AB=BP=3����x=3��
��ii����AP=FP�����APF=120�㣾90�㣨��ȥ����
��iii����AP=AF�����CBP=��CPB=75�㣬BC=PC����ʱx=3![]() .
.


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
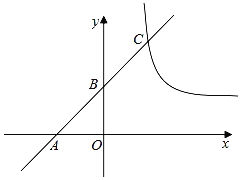
����Ŀ����֪����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB��x�ύ�ڵ�A����2��0������y��������ύ�ڵ�B���뷴��������y��![]() ��x��0����ͼ���ڵ�C����AB��BC����C��������Ϊ4��
��x��0����ͼ���ڵ�C����AB��BC����C��������Ϊ4��
��1����ֱ��AB�ı���ʽ��
��2������B��BD��x�ᣬ������������y��![]() ��ͼ���ڵ�D�����߶�CD�ij��ȣ�
��ͼ���ڵ�D�����߶�CD�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
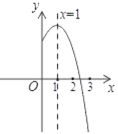
����Ŀ��������y��ax2+bx+c�IJ���ͼ����ͼ��ʾ��ֱ��x��1Ϊ�Գ��ᣬ���½��ۢ�a��0����b��0����2a+b��0����3a+c��0��ȷ���У�����ţ�_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
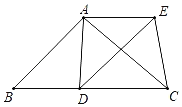
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����D�ڱ�BC�ϣ�����AD����ADΪһ������ADE������AD��AE����DAE����BAC������EC��
��1����֤��CAƽ�֡�DCE��
��2�����AB2��BDBC����֤���ı���ABDE��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=CB����ABC=90����DΪAB�ӳ�����һ�㣬��E��BC���ϣ���BE=BD������AE��DE��DC

����֤����ABE�ա�CBD��
������CAE=30�������BDC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ��ȤС���У������������λͬѧ�������ͼ��ʾ������ת������Ϸ��ÿ��ת�̱��ֳ������ȵļ������Σ�����ÿ�����������ڱ������֣�����Ϸ�������£����˷ֱ�ͬʱת���ס���ת�̣�ת��ֹͣ����ָ����ָ������������С��12���������ʤ����ָ����ָ�����������͵���12����Ϊƽ�֣���ָ����ָ�����������ʹ���12����������ʤ����ָ��ͣ�ڵȷ����ϣ���תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ����
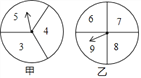
��1�������б��ķ�����ʾ��������Ϸ�������͵����п��ܵĽ����
��2���ֱ���������������ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������״�����������鷢����ȫ����������������ع�����ij��Ϊ�˾������100��ֻ���ֵ����������żס���������������ɣ���֪�׳�ÿ�����������ֵ��������ҳ�ÿ�����������ֵ�������1.5���������ڶ������60��ֻ���ֵ���������ʱ���׳����ҳ�����5�죮������Ӧ��������������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
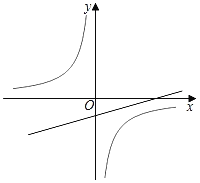
����Ŀ����ͼ����ƽ��ֱ������ϵ��AΪֱ��y=![]() x��1��һ�㣬��ԭ��O��ֱ���뷴��������y=��
x��1��һ�㣬��ԭ��O��ֱ���뷴��������y=��![]() ͼ���ڵ�B��C������ABCΪ�ȱ������Σ����A������Ϊ_____��
ͼ���ڵ�B��C������ABCΪ�ȱ������Σ����A������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У��Խ���AC��BD���ֱ��AC=4��BD=6��˳����������ı����е����õ��ı��ε��������________
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com