
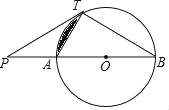
【题目】如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.
(1)求证:PT2=PAPB;
(2)若PT=TB=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析。(2)![]() .
.
【解析】
试题分析:(1)连接OT,只要证明△PTA∽△PBT,可得![]() ,由此即可解决问题;
,由此即可解决问题;
(2)首先证明△AOT是等边三角形,根据S阴=S扇形OAT﹣S△AOT计算即可;
试题解析:(1)证明:连接OT.
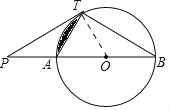
∵PT是⊙O的切线,
∴PT⊥OT,
∴∠PTO=90°,
∴∠PTA+∠OTA=90°,
∵AB是直径,
∴∠ATB=90°,
∴∠TAB+∠B=90°,
∵OT=OA,
∴∠OAT=∠OTA,
∴∠PTA=∠B,∵∠P=∠P,
∴△PTA∽△PBT,
∴![]() ,
,
∴PT2=PAPB.
(2)∵TP=TB=![]() ,
,
∴∠P=∠B=∠PTA,
∵∠TAB=∠P+∠PTA,
∴∠TAB=2∠B,
∵∠TAB+∠B=90°,
∴∠TAB=60°,∠B=30°,
∴tanB=![]()
∴AT=1,
∵OA=OT,∠TAO=60°,
∴△AOT是等边三角形,
∴S阴=S扇形OAT﹣S△AOT=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( ) 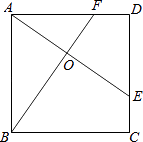
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成题目:
(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写作法,保留作图痕迹);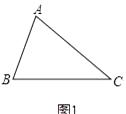
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;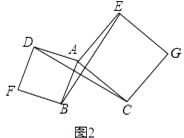
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.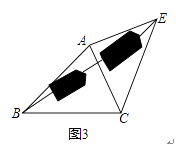
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,AE=CF. 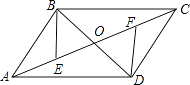
(1)求证:△BOE≌△DOF;
(2)连接DE、BF,若BD⊥EF,试探究四边形EBDF的形状,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.

(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com