
ij������50�����乩�ο;�ס����ÿ������ÿ��Ķ���Ϊ180Ԫʱ�������ȫ��ע������ÿ������ÿ��Ķ�������10Ԫʱ���ͻ���һ��������У�����ο;�ס���䣬�������ÿ������ÿ��֧��20Ԫ�ĸ��ַ��ã������۶�λ����Ԫʱ���������������������Ƕ��٣���ÿ�����䶨������10xԪ������ÿ�������ΪyԪ��
�����������������е�������ϵ���ú�x��ʽ�������
|
| ԭ�� | ÿ����������10Ԫ | ÿ����������20Ԫ | �� | ÿ����������10xԪ |
| ÿ�����۶��� | 180 | 190 | 200 | �� |
|
| ��ס�������� | 50 | 49 | 48 | �� |
|
���������Ϸ������ú�x��ʽ�ӱ�ʾy�����������Ľ⣮
�����㡿���κ�����Ӧ�ã�
����������1������ÿ������ķ���ÿ����10xԪ�����䶨�ۣ�180+10x��Ԫ������ٷ���x�䣬��ס����������50��x���䣻
��2�����ݣ�1���д���ʽ������ÿ�������Ϊy=�����䶨�۩�ÿ��֧�����ã�����ס����������
����𡿽⣺��1��������£�
|
| ԭ�� | ÿ����������10Ԫ | ÿ����������20Ԫ | �� | ÿ����������10xԪ |
| ÿ�����۶��� | 180 | 190 | 200 | �� | 180+10x |
| ��ס�������� | 50 | 49 | 48 | �� | 50��x |
��2��y=��180+10x��20������50��x��=��10x2+340x+8000=��10��x��17��2+10890��
��x=17ʱ��180+10x=350��50��x=33��
���Ե����۶�Ϊ350Ԫʱ����������������������10890Ԫ��
��������������Ҫ�����˶��κ�����Ӧ�ã��ر����׳��ֵĴ�����������ֵʱ������x�ķ�Χ��ֱ�������꣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����P����x��ĶԳƵ�ΪP1��2a+b��3��������y��ĶԳƵ�ΪP2��9��b+2�������P������Ϊ��������
A����9��3�� B������9��3�� C����9����3�� D������9����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ABCD�У�AD=8cm��AB=6cm������E�ӵ�C��ʼ�ر�CB���B��2cm/s���ٶ��˶�������F�ӵ�Cͬʱ�����ر�CD���D��1cm/s���ٶ��˶�����Dֹͣ����ͼ�ɵõ�����CFHE�����˶�ʱ��Ϊx����λ��s������ʱ����ABCDȥ������CFHE��ʣ�ಿ�ֵ����Ϊy����λ��cm2������y��x֮��ĺ�����ϵ��ͼ���ʾ��������ͼ�еģ�������
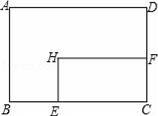

A��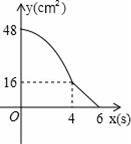
 B��
B��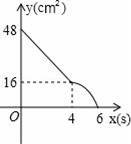
 C��
C��
 D��
D��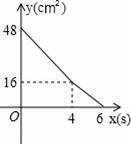

��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ������������������һ���߳�Ϊ4��ƽ���ı���ABCD
����ƽ���ı���ABCD���������������������
����������ͼ��ʾ�������У������ƴ��һ����һ�߳�Ϊ6�ľ��Σ������ü��ߣ������������������ƴ�ӷ�����������������
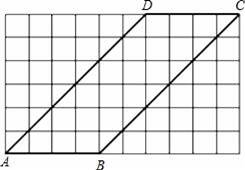

��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������x-2=0�Ľ�Ҳ��ֱ��y=(2k-1)x+10��x��Ľ���ĺ����꣬��k��ֵΪ
A.2 B.0 C.-2 D. ��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪һ��ƽ���ı������ڱߵij��ֱ�Ϊ10��6,��ô�����ܳ�Ϊ( ).
A. 16 B. 60 C.32 D. 30
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
.ij��λ�����ڲ���Ƹ������Աһ�����Լס��ҡ���������ѡ �˽����˱��Ժ�����������ԣ����˵IJ��Գɼ����±���ʾ.
 |
| ���� ��Ŀ | ���Գɼ�/�� | ||
| �� | �� | �� | |
| ���� | 75 | 800 | 90 |
| ���� | 93 | 70 | 68 |
����¼�ó�����֯200��ְ������������Ͷ���Ƽ��ķ�ʽ�����������飬���˵�Ʊ�ʣ�û����ȨƱ��ÿλְ��ֻ���Ƽ�1�ˣ�����ͼ��ʾ��ÿ��һƱ����1�֡�
��1����������˵���������÷֣�
��2���������������Ե�ƽ���ɼ�ȷ��¼����ѡ����ô˭��¼�ã���ȷ��0.01����
��3������ʵ����Ҫ����λ�����ԡ����ԡ���������������Ե÷ְ�4:3:3�ı���ȷ�����˳ɼ�����ô˭����¼�ã�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com