
【题目】如图,已知∠AOB等于30°,角内有一点P,OP=6,点M在OA上,点N在OB上,△PMN周长的最小值是 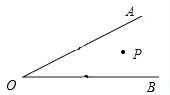
【答案】6
【解析】解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=6,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=6.
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=6.
所以答案是:6.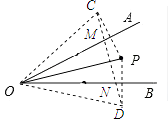
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


科目:初中数学 来源: 题型:
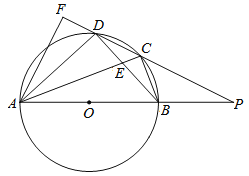
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,若PB=OB,CD=![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)OA= cm,OB= cm.
(2)若点C是线段AO上一点,且满足AC=CO+CB,求CO的长.
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为t(s),当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP﹣OQ=8.
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后立即返回,又以同样的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠CAB=∠DAB,则添加下列一个条件不能使△ABC≌△ABD的是( ) 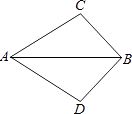
A.AC=AD
B.BC=BD
C.∠C=∠D
D.∠ABC=∠ABD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲地宏达物流公司的快递车和货车同时从甲地出发,以各自的速度沿快速通道向乙地匀速行驶, 快递车到达乙地后,卸完物资并另装货物共用了 45 分钟,然后按原路以另一速度返回,直至与货车相遇.已知货车行驶速度为 60 km/h,两车间的距离 y(km) 与货车行驶时间 x(h) 之间的函数图象如图所示:
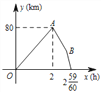
给出以下四个结论:
① 快递车从甲地到乙地的速度是 100 km/h;
② 甲、乙两地之间的距离是 80 km;
③ 图中点 B 的坐标为 (![]() , 35);
, 35);
④ 快递车从乙地返回时的速度为 90 km/h.
其中正确的是_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线. 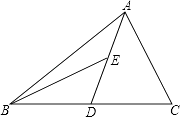
(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为40,BD=5,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com