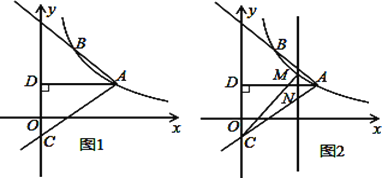
【题目】如图1，反比例函数的图象经过点A（，1），射线AB与反比例函数图象交与另一点B（1， ），射线AC与轴交于点C， 轴，垂足为D．

（1）求和a的值；

（2）直线AC的解析式；

（3）如图2，M是线段AC上方反比例函数图象上一动点，过M作直线轴，与AC相交于N，连接CM，求面积的最大值．

参考答案：

【答案】（1）；（2）y=x﹣1；（3）

【解析】试题分析：（1）把A点代入反比例函数解析式可求得k，把B点坐标代入反比例函数解析式可求得a的值；

（2）过B作BH⊥AD于H，由A、B坐标可得出△ABH为等腰直角三角形，由条件可求得∠DAC=30°，在△ACD中，由勾股定理可求得CD、AC，可求得C点坐标，利用待定系数法可求得直线AC的解析式；

（3）可设出M点坐标为（t， ），从而可表示出N点坐标，则可用t表示出MN的长，则可用t表示出△CMN的面积，利用二次函数的性质可求得其最大值．

试题解析：（1）把A（2，1）代入y=，可得k=2×1=2，

∴反比例函数解析式为y=，

把B（1，a）代入反比例函数解析式y=，可得a=2；

（2）作BH⊥AD于H，如图1，

∵B点坐标为（1，2），

∴AH=2-1，BH=2-1，

∴△ABH为等腰直角三角形，

∴∠BAH=45°，

∵∠BAC=75°，

∴∠DAC=∠BAC-∠BAH=30°，

∵AD=2，设CD=x，则AC=2x，

∴由勾股定理可得CD=2，AC=4，

∴C点坐标为（0，-1），

设直线AC解析式为y=kx+b，

把A（2，1），C（0，-1）代入可得

，解得，

∴直线AC解析式为y=x-1；

（3）设M点坐标为（t， ）（0＜t＜1），

∵直线l⊥x轴，与AC相交于点N，

∴N点坐标为（t， t-1），

∴MN=-（t-1）=-t+1，

∴S△CMN=t（-t+1）=-t2+t+，

∴当t=-=时，S有最大值，最大值为．

关闭