【题目】如图，在四边形ABCD中，对角线AC与BD相交于点E，若AC平分∠DAB，且AB＝AC，AC＝AD，有如下四个结论：①AC⊥BD；②BC＝DE；③∠DBC＝∠DAC；④△ABC是正三角形．请写出正确结论的序号___________（把你认为正确结论的序号都填上）
期末冲刺100分创新金卷完全试卷系列答案科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如下图所示，且关于x的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论：①b2-4ac>0；②abc<0；③m>2.其中，正确结论的个数是
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目：初中数学 来源： 题型：
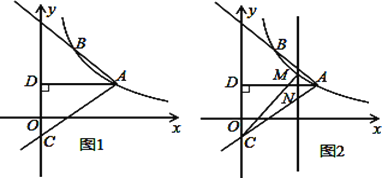
【题目】如图1，反比例函数
的图象经过点A（
，1），射线AB与反比例函数图象交与另一点B（1， 
），射线AC与
轴交于点C， 
轴，垂足为D．
（1）求
和a的值；
（2）直线AC的解析式；
（3）如图2，M是线段AC上方反比例函数图象上一动点，过M作直线
轴，与AC相交于N，连接CM，求
面积的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】地表以下岩层的温度t (℃)，随着所处的深度 h (km)的变化而变化，t与h 在一定范围内近似成一次函数关系．
(1)根据下表，求 t(℃)与h (km)之间的函数关系式.
(2)求当岩层温度达到 1770 ℃时，岩层所处的深度为多少千米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y＝ax2＋bx＋c（a≠0）图象如图，下列结论：① abc＞0；② 2a＋b＝0；③ 当m≠1时，a＋b＞am2＋bm；④ a－b＋c＞0；⑤若ax12＋bx1＝ax22＋bx2，且x1≠x2，x1＋x2＝2，
其中正确的有（ ）
A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC,AD=AE,C,D,E在同一条直线上，连结BD,BE.有以下结论①△ACE≌△BCD;②BD=CE;③∠ADB=45°;④∠ACE+∠DBC=45°.其中正确结论的是_________.（写上序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图所示，甲、乙、丙三个人做传球游戏，游戏规则如下：甲将球传给乙，乙将球立刻传给丙，然后丙又立刻将球传给甲．若甲站在∠AOB内的P点，乙站在OA上，丙站在OB上，并且甲、乙、丙三人的传球速度相同．问乙和丙必须站在何处，才能使球从甲到乙、乙到丙、最后丙到甲这一轮所用的时间最少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB=3，AD=1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于M，则点M的表示的数为________________．
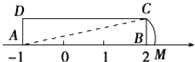
【答案】
【解析】AC＝AM＝
＝
，∴AM＝
【题型】填空题
【结束】
11
【题目】在△ABC中，AB＝10，AC＝2，BC边上的高AD＝6，则另一边BC等于_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（－3，5），B（－2，1），C（－1，3）．
（1）画出△ABC关于x轴的对称图形△A1B1C1；
（2）画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2；
（3）如果AC上有一点M（a，b）经过上述两次变换，那么对应A2C2上的点M2的坐标是 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
