
【题目】如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.
①如图1,若∠MON=150°,求证:△ABR为等边三角形;
②如图3,若△ARB∽△PEQ,求∠MON大小和 ![]() 的值.
的值.
【答案】
(1)
证明:∵点C、D、E分别是OA,OB,AB的中点,
∴DE=OC,∥OC,CE=OD,CE∥OD,
∴四边形ODEC是平行四边形,
∴∠OCE=∠ODE,
∵△OAP,△OBQ是等腰直角三角形,
∴∠PCO=∠QDO=90°,
∴∠PCE=∠PCO+∠OCE=∠QDO=∠ODQ=∠EDQ,
∵PC= ![]() AO=OC=ED,CE=OD=
AO=OC=ED,CE=OD= ![]() OB=DQ,
OB=DQ,
在△PCE与△EDQ中, 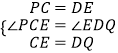 ,
,
∴△PCE≌△EDQ;
(2)
解:①如图2,
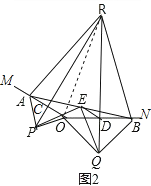
连接RO,
∵PR与QR分别是OA,OB的垂直平分线,
∴AP=OR=RB,
∴∠ARC=∠ORC,∠ORQ=∠BRO,
∵∠RCO=∠RDO=90°,∠COD=150°,
∴∠CRD=30°,
∴∠ARB=60°,
∴△ARB是等边三角形;
②由(1)得,EQ=EP,∠DEQ=∠CPE,
∴∠PEQ=∠CED﹣∠CEP﹣∠DEQ=∠ACE﹣∠CEP﹣∠CPE=∠ACE﹣∠RCE=∠ACR=90°,
∴△PEQ是等腰直角三角形,
∵△ARB∽△PEQ,
∴∠ARB=∠PEQ=90°,
∴∠OCR=∠ODR=90°,∠CRD= ![]() ∠ARB=45°,
∠ARB=45°,
∴∠MON=135°,
此时P,O,B在一条直线上,△PAB为直角三角形,且∠APB=90°,
∴AB=2PE=2× ![]() PQ=
PQ= ![]() PQ,
PQ,
∴ ![]() =
= ![]()
【解析】(1)根据三角形中位线的性质得到DE=OC,∥OC,CE=OD,CE∥OD,推出四边形ODEC是平行四边形,于是得到∠OCE=∠ODE,根据等腰直角三角形的定义得到∠PCO=∠QDO=90°,根据等腰直角三角形的性质得到得到PC=ED,CE=DQ,即可得到结论(2)①连接RO,由于PR与QR分别是OA,OB的垂直平分线,得到AP=OR=RB,由等腰三角形的性质得到∠ARC=∠ORC,∠ORQ=∠BRO,根据四边形的内角和得到∠CRD=30°,即可得到结论;
②由(1)得,EQ=EP,∠DEQ=∠CPE,推出∠PEQ=∠ACR=90°,证得△PEQ是等腰直角三角形,根据相似三角形的性质得到ARB=∠PEQ=90°,根据四边形的内角和得到∠MON=135°,求得∠APB=90°,根据等腰直角三角形的性质得到结论.本题考查了相似三角形的判定和性质,等腰直角三角形的性质,全等三角形的判定和性质,平行四边形的判定和性质,等边三角形的判定和性质,线段垂直平分线的性质,熟练掌握等腰直角三角形的性质是解题的关键.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车公司调查阳光中学学生对其产品的了解情况,随机抽取部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图.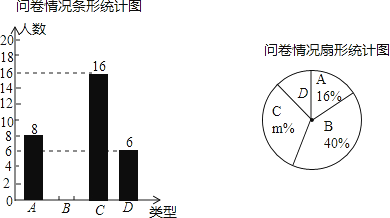
(1)本次问卷共随机调查了名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图.
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC(不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,若BP=3,求△ABP的周长;
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并说明理由;
(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,则B′D=_____.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求回答问题
(1)观察下列图形与等式的关系,并填空:
(2)观察下图,根据(1)中结论,计算图中黑球的个数,用含有n的代数式填空:
1+3+5+…+(2n﹣1)+()+(2n﹣1)+…+5+3+1= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解本校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、排球、其它等四个方面调查了若干名学生,并绘制成“折线统计图”与“扇形统计图”.请你根据图中提供的部分信息解答下列问题: 

(1)在这次调查活动中,一共调查了名学生;
(2)“足球”所在扇形的圆心角是度;
(3)补全折线统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系XOY中,直线l1过点A(1,0)且与y轴平行,直线l2过点B(0,2)且与x轴平行,直线l1与直线l2相交于点P.点E为直线l2上一点,反比例函数 ![]() (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F. 
(1)若点E与点P重合,求k的值;
(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积的2倍,求E点的坐标;
(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求E点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形纸片ABC的∠C为90°,将三角形纸片沿着图示的中位线DE剪开,然后把剪开的两部分重新拼接成不重叠的图形,下列选项中不能拼出的图形是( ) 
A.平行四边形
B.矩形
C.等腰梯形
D.直角梯形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com