
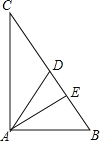
【题目】如图,Rt△ABC中,∠A=90°,AD、AE分别是BC边的中线和高,若cosB=![]() ,BC=10.
,BC=10.
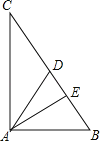
(1)求AB的长;
(2)求AE的长;
(3)求sin∠ADB的值.
【答案】(1)6;(2)![]() ;(3)
;(3)![]()
【解析】
(1)在Rt△ABC中,通过解直角三角形可求出AB的长;
(2)在Rt△ABC中,利用勾股定理可求出AC的长,再利用面积法可求出AE的长;
(3)利用直角三角形斜边上的中线等于斜边的一半可求出AD的长,在Rt△AED中,利用正弦的定义可求出sin∠ADB的值.
解:(1)在Rt△ABC中,∠A=90°,cosB=![]() ,BC=10,
,BC=10,
∴AB=BCcosB=10×![]() =6.
=6.
(2)在Rt△ABC中,∠A=90°,BC=10,AB=6,
∴AC=![]() =
=![]() =8.
=8.
∵AE是BC边的高,
∴![]() ACAB=
ACAB=![]() BCAE,即
BCAE,即![]() ×8×6=
×8×6=![]() ×10AE,
×10AE,
∴AE=![]() .
.
(3)Rt△ABC中,AD是BC边的中线,BC=10,
∴AD=![]() BC=5.
BC=5.
在Rt△AED中,∠AED=90°,AD=5,AE=![]() ,
,
∴sin∠ADB=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
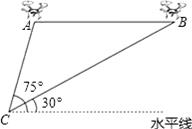
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一幅长为60 cm,宽为40 cm的矩形风景画的四周镶一条相同宽度的纸边,制成一幅矩形挂图.若要使整个挂图的面积是3 500 cm2,设纸边的宽为x cm,则根据题意可列方程为( )

A. (60+x)(40+x)=3 500 B. (60+2x)(40+2x)=3 500
C. (60-x)(40-x)=3 500 D. (60-2x)(40-2x)=3 500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年种植了10亩地的南瓜,亩产量为2000![]() ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间满足关系:
(元)之间满足关系:![]() ,其图像如图所示.
,其图像如图所示.
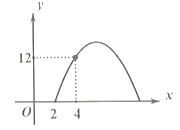
(1)销售单价为多少元时,这种商品每天的销售利润最大?最大利润为多少元?
(2)若该商品每天的销售利润不低于12元,则销售单价![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在一次社会实践活动中,通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律:
①该蔬菜的销售价![]() (单位:元/千克)与时间
(单位:元/千克)与时间![]() (单位:月份)满足关系:
(单位:月份)满足关系: ![]() ;
;
②该蔬菜的平均成本![]() (单位:元/千克)与时间
(单位:元/千克)与时间![]() (单位:月份)满足二次函数关系
(单位:月份)满足二次函数关系![]() .已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
.已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
(1)求该二次函数的解析式;
(2)请运用小明统计的结论,求出该蔬菜在第几月份的平均利润![]() (单位:元/千克)最大?最大平均利润是多少?(注:平均利润
(单位:元/千克)最大?最大平均利润是多少?(注:平均利润![]() 销售价
销售价![]() 平均成本)
平均成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1矩形ABCD中,点E是CD边上的动点(点E不与点C,D重合),连接AE,过点A作AF⊥AE交CB延长线于点F,连接EF,点G为EF的中点,连接BG.
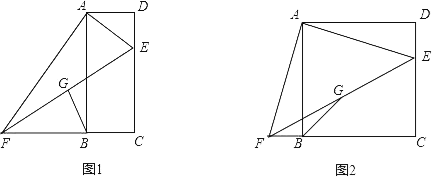
(1)求证:△ADE∽△ABF;
(2)若AB=20,AD=10,设DE=x,点G到直线BC的距离为y.
①求y与x的函数关系式;②当![]() 时,x的值为 ;
时,x的值为 ;
(3)如图2,若AB=BC,设四边形ABCD的面积为S,四边形BCEG的面积为S1,当![]() 时,DE:DC的值为 .
时,DE:DC的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山民居(记为C)、李庄古镇(记为D)的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点都被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为 .
(2)用树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com