
����Ŀ����֪�ı���ABCD��һ��Ա�AD��BC���ӳ��߽��ڵ�E��
��1����ͼ1������ABC=��ADC=90�㣬��֤��EDEA=ECEB��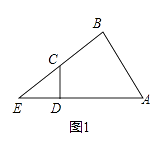
��2����ͼ2������ABC=120�㣬cos��ADC= ![]() ��CD=5��AB=12����CDE�����Ϊ6�����ı���ABCD�������
��CD=5��AB=12����CDE�����Ϊ6�����ı���ABCD�������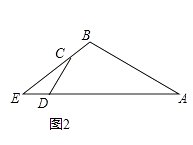
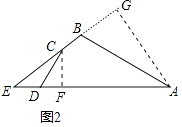
��3����ͼ3����һ��Ա�AB��DC���ӳ����ཻ�ڵ�F����cos��ABC=cos��ADC= ![]() ��CD=5��CF=ED=n��ֱ��д��AD�ij����ú�n��ʽ�ӱ�ʾ��
��CD=5��CF=ED=n��ֱ��д��AD�ij����ú�n��ʽ�ӱ�ʾ��
���𰸡�
��1���⣺��ͼ1�У�
�ߡ�ADC=90�㣬��EDC+��ADC=180�㣬
���EDC=90�㣬
�ߡ�ABC=90�㣬
���EDC=��ABC��
�ߡ�E=��E��
���EDC�ס�EBA��
�� ![]() =
= ![]() ��
��
��EDEA=ECEB��
��2���⣺��ͼ2�У���C��CF��AD��F��AG��EB��G��
��Rt��CDF��cos��ADC= ![]() ��
��
�� ![]() =
= ![]() ����CD=5��
����CD=5��
��DF=3��
��CF= ![]() =4��
=4��
��S��CDE=6��
�� ![]() EDCF=6��
EDCF=6��
��ED= ![]() =3��EF=ED+DF=6��
=3��EF=ED+DF=6��
�ߡ�ABC=120�㣬��G=90�㣬��G+��BAG=��ABC��
���BAG=30�㣬
����Rt��ABG��BG= ![]() AB=6��AG=
AB=6��AG= ![]() =6
=6 ![]() ��
��
��CF��AD��AG��EB��
���EFC=��G=90�㣬�ߡ�E=��E��
���EFC�ס�EGA��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��EG=9 ![]() ��
��
��BE=EG��BG=9 ![]() ��6��
��6��
��S�ı���ABCD=S��ABE��S��CDE= ![]() ��9
��9 ![]() ��6����6
��6����6 ![]() ��6=75��18
��6=75��18 ![]() ��
��
��3���⣺��ͼ3�У���CH��AD��H����CH=4��DH=3��

��tan��E= ![]() ��
��
��AG��DF�ڵ�G����AD=5a����DG=3a��AG=4a��
��FG=DF��DG=5+n��3a��
��CH��AD��AG��DF����E=��F��
��֤��AFG�ס�CEH��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��a= ![]() ��
��
��AD=5a= ![]() ��
��
��������Ҫ֤�˻�ʽ��ʽ�������ɻ�Ϊ����ʽ��![]() ��������һ��ȷ�������Ρ�EDC���EBA���ƣ���2������ǡ����Ǻ���Ӧ����ֱ�������������ã�����������߹���ֱ�������Σ�ǡ�ù�����ڣ�1�����ͼ�Σ������һ�ʵ�˼·�����EG����һ���������֮�����ı���ABCD�����.��3�������߹����ֱ�������Σ��������������Ρ�AFG�ס�CEH����������ʽ�����AD�ij�.
��������һ��ȷ�������Ρ�EDC���EBA���ƣ���2������ǡ����Ǻ���Ӧ����ֱ�������������ã�����������߹���ֱ�������Σ�ǡ�ù�����ڣ�1�����ͼ�Σ������һ�ʵ�˼·�����EG����һ���������֮�����ı���ABCD�����.��3�������߹����ֱ�������Σ��������������Ρ�AFG�ס�CEH����������ʽ�����AD�ij�.
�����㾫�����������⣬������Ҫ�˽����������ε��ж�������(���������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ��)����Ҫ����������Ǻ����Ķ���(���A�����ҡ����ҡ����С����ж�������A��������Ǻ���)�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����ǰ尴��ͼ1��ʽƴ����һ�����б�OA��OC��ֱ��EF�غϣ�![]() ��
��![]()
![]() ͼ1��
ͼ1��![]() ______
______![]()
![]() ��ͼ2�����ǰ�COD�̶������������ǰ�AOB���ŵ�O��˳ʱ�뷽����תһ���Ƕ�
��ͼ2�����ǰ�COD�̶������������ǰ�AOB���ŵ�O��˳ʱ�뷽����תһ���Ƕ�![]() ����ת���������������ǰ嶼��ֱ��EF���Ϸ���
����ת���������������ǰ嶼��ֱ��EF���Ϸ���
![]() ��OBƽ��OA��OC��OD���е�������ɵĽ�ʱ��������Ҫ���������ת�Ƕ�
��OBƽ��OA��OC��OD���е�������ɵĽ�ʱ��������Ҫ���������ת�Ƕ�![]() ��ֵ��
��ֵ��
![]() �Ƿ����
�Ƿ����![]() �������ڣ����ʱ��
�������ڣ����ʱ��![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx��2��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����A������Ϊ��4��0�����ҵ�x=��2��x=5ʱ���κ����ĺ���ֵy��ȣ�
��1����ʵ��a��b��ֵ��
��2����ͼ1������E��Fͬʱ��A����������е�E��ÿ��2����λ���ȵ��ٶ���AB�����յ�B�˶�����F��ÿ�� ![]() ����λ���ȵ��ٶ�������AC�����˶�������Eֹͣ�˶�ʱ����F��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����EF������AEF��EF���ۣ�ʹ��A���ڵ�D�����õ���DEF��
����λ���ȵ��ٶ�������AC�����˶�������Eֹͣ�˶�ʱ����F��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����EF������AEF��EF���ۣ�ʹ��A���ڵ�D�����õ���DEF��
���Ƿ����ijһʱ��t��ʹ�á�DCFΪֱ�������Σ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�����DEF���ABC�ص����ֵ����ΪS����S����t�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ��е�����ֱ�����ǰ��ֱ�Ƕ���C����ͼ��ʽ������һ��������ʾ����A��60�㣬��D��30�㣬��E����B��45�㣮
(1)������DCB��45�㣬���ACB�Ķ���Ϊ�� ����
������ACB��140�㣬���DCE�Ķ���Ϊ�� ����
(2)��(1)�����ACB���DCE��������ϵ����˵�����ɣ�
(3)����ACE��90���ҵ�E��ֱ��AC���Ϸ�ʱ�������������dz���һ�����ƽ��ʱ����ֱ��д����ACE�Ƕ����п��ܵ�ֵ(����˵������)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ܺ���Ӱ�죬�Ա����ϵĵ���ȡů�����ۻ�����ij��������ÿ̨�ɱ��۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ���ȡů�����±��ǽ���������������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3100Ԫ |
�����ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
��1����A��B�����ͺŵĵ���ȡů�������۵��ۣ�
��2�����������ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȡů����30̨����A���ͺŵĵ���ȡů������ܲɹ�����̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A����1��1����B��4��6����������y=ax2+bx��
��1���������ߵĽ���ʽ��
��2����ͼ1����F������Ϊ��0��m����m��2����ֱ��AF������������һ��G������G��x��Ĵ��ߣ�����ΪH������������x��������ύ�ڵ�E������FH��AE����֤��FH��AE��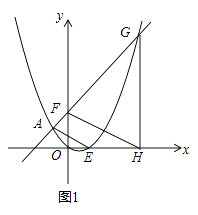
��3����ͼ2��ֱ��AB�ֱ�x�ᡢy����C��D���㣮��P�ӵ�C������������CD���������˶����ٶ�Ϊÿ�� ![]()
����λ���ȣ�ͬʱ��Q��ԭ��O��������x�������������˶����ٶ�Ϊÿ��1����λ���ȣ���M��ֱ��PQ�������ߵ�һ�����㣬���˶���t��ʱ��QM=2PM��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶(1)�������ίԱ�ڰ�ڰ屨ʱ,�����������ͼ����Ϊ�߿�,����ÿ����ɫ��������6����ɫ��������������һ�α߿�����25����ɫ������,����α߿��а�ɫ������

A. 100�� B. 102�� C. 98�� D. 150��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
����С������8�֣�ijѧУ��֯���꼶ѧ���μ����ʵ���������������35���ͳ�����������պ�����������������55���ͳ������������һ��������45������λ��
��1�����У���꼶ѧ���μ����ʵ�����������
��2����֪35���ͳ������Ϊÿ��320Ԫ��55���ͳ������Ϊÿ��400Ԫ��������ʽ���1500Ԫ��Ԥ�㣬ѧУ����ͬʱ���������ֿͳ���4������������������������㱾�����ʵ������賵�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������鹤��ͬʱ�ӹ�ij����������鹤������һ��ͣ�������豸�������豸
������Ĺ���Ч����ԭ����2����������Լӹ����������![]() (��)��ʱ��
(��)��ʱ��![]() (ʱ)�ĺ���ͼ
(ʱ)�ĺ���ͼ
����ͼ��ʾ��
��1�������ӹ����������y��ʱ��![]() ֮��ĺ�����ϵʽ����2�֣�
֮��ĺ�����ϵʽ����2�֣�
��2��������ӹ��������![]() ��ֵ����3�֣�
��ֵ����3�֣�
��3���ס�������ӹ������������һ��װ�䣬ÿ��300��װһ�䣬���װ���ʱ����Բ��ƣ����ʱ��ǡ��װ����1�䣿�پ����ʱ��ǡ��װ����2�䣿��5�֣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com