
【题目】已知一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,![]() ,
,![]()
![]() 图1中
图1中![]() ______
______![]()
![]() 如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度
如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度![]() ,在转动过程中两块三角板都在直线EF的上方:
,在转动过程中两块三角板都在直线EF的上方:
![]() 当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度
当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度![]() 的值;
的值;
![]() 是否存在
是否存在![]() ?若存在,求此时的
?若存在,求此时的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

【答案】(1)75(2)①![]() ,
,![]() ,
,![]() ②当
②当![]() 或
或![]() 时,存在
时,存在![]()
【解析】
(1)根据平平角的定义即可得到结论;
(2)①根据已知条件和角平分线的定义即可得到结论;
②当OA在OD的左侧时,当OA在OD的右侧时,列方程即可得到结论.
解:(1)∵∠AOB=45°,∠COD=60°,
∴∠BOD=180°∠AOB∠COD=75°,
故答案为:75;
(2)①当OB平分∠AOD时,
∵∠AOE=α,∠COD=60°,
∴∠AOD=180°∠AOE∠COD=120°α,
∴∠AOB=![]() ∠AOD=60°
∠AOD=60°![]() α=45°,
α=45°,
∴α=30°,
当OB平分∠AOC时,
∵∠AOC=180°α,
∴∠AOB═90°![]() α=45°,
α=45°,
∴α=90°;
当OB平分∠DOC时,
∵∠DOC=60°,
∴∠BOC=30°,
∴α=180°45°30°=105°,
综上所述,旋转角度α的值为30°,90°,105°;
②当OA在OD的左侧时,则∠AOD=120°α,∠BOC=135°α,
∵∠BOC=2∠AOD,
∴135°α=2(120°α),
∴α=105°;
当OA在OD的右侧时,则∠AOD=α120°,∠BOC=135°α,
∵∠BOC=2∠AOD,
∴135°α=2(α120),
∴α=125°,
综上所述,当α=105°或125°时,存在∠BOC=2∠AOD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.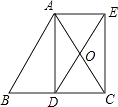
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
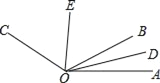
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是(用含m的代数式表示)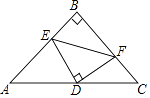
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() .
.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若![]() 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;
A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,某市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的一组对边AD、BC的延长线交于点E.
(1)如图1,若∠ABC=∠ADC=90°,求证:EDEA=ECEB;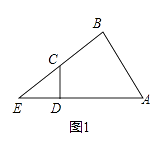
(2)如图2,若∠ABC=120°,cos∠ADC= ![]() ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;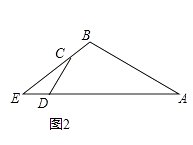
(3)如图3,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC= ![]() ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com