
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() .
.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若![]() 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;
A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
【答案】(1)当x=1时,y=3;当x=2时,y=1(2)C(3)有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;或购买单价为3元的笔记本10本,单价为5元的钢笔1支.
【解析】
根据题意可知,求方程的正整数解,先把方程做适当的变形,再列举正整数代入求解.(1)(2)参照例题的解题思路进行解答;
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.则根据题意得:3m+5n=35,其中m、n均为自然数.参照例题的解题思路解该二元一次方程即可.
解:(1)由2x+y=5,得y=5-2x(x、y为正整数).
所以![]() ,即0<x<
,即0<x<![]()
∴当x=1时,y=3;
当x=2时,y=1.
即方程的正整数解是![]() 或
或![]() ;
;
(2)同样,若![]() 为自然数,
为自然数,
则有:0<x-2≤6,即2<x≤8.
当x=3时,![]() ;
;
当x=4时,![]() ;
;
当x=5时,![]() ;
;
当x=8时,![]() .
.
即满足条件x的值有4个,
故选C;
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.
则根据题意得:3m+5n=35,其中m、n均为自然数.
于是有:![]() ,
,
解得: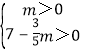 ,
,
所以0<m<![]() .
.
由于n=7-![]() m为正整数,则
m为正整数,则![]() m为正整数,可知m为5的倍数.
m为正整数,可知m为5的倍数.
∴当m=5时,n=4;
当m=10时,n=1.
答:有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;
或购买单价为3元的笔记本10本,单价为5元的钢笔1支.
故答案为:(1)当x=1时,y=3;当x=2时,y=1;(2)C;(3)有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;或购买单价为3元的笔记本10本,单价为5元的钢笔1支.


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
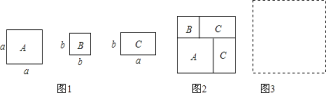
【题目】现有若干张如图1所示的正方形纸片A,B和长方形纸片C.
(1)小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式:______ ;
(2)小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是______ ,并请你在图3位置画出拼成的长方形;
(3)根据拼图经验,请将多项式a2+5ab+4b2分解因式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+1经过A(﹣1,0),B(1,1)两点.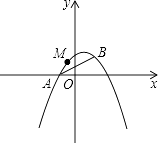
(1)求该抛物线的解析式;
(2)阅读理解:
在同一平面直角坐标系中,直线l1:y=k1x+b1(k1 , b1为常数,且k1≠0),直线l2:y=k2x+b2(k2 , b2为常数,且k2≠0),若l1⊥l2 , 则k1k2=﹣1.
解决问题:
①若直线y=3x﹣1与直线y=mx+2互相垂直,求m的值;
②抛物线上是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,![]() ,
,![]()
![]() 图1中
图1中![]() ______
______![]()
![]() 如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度
如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度![]() ,在转动过程中两块三角板都在直线EF的上方:
,在转动过程中两块三角板都在直线EF的上方:
![]() 当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度
当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度![]() 的值;
的值;
![]() 是否存在
是否存在![]() ?若存在,求此时的
?若存在,求此时的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
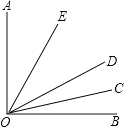
【题目】如图,已知∠AOB内部有三条射线,OE平分∠AOD,OC平分∠BOD.
(1)若∠AOB=90°,求∠EOC的度数;
(2)若∠AOB=α,求∠EOC的度数;
(3)如果将题中“平分”的条件改为∠EOA=![]() ∠AOD,∠DOC=
∠AOD,∠DOC=![]() ∠DOB且∠DOE:∠DOC=4:3,∠AOB=90°,求∠EOC的度数.
∠DOB且∠DOE:∠DOC=4:3,∠AOB=90°,求∠EOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(![]() ,0),B(2,0),直线y=kx+b经过B,D两点.
,0),B(2,0),直线y=kx+b经过B,D两点.
(1)求直线y=kx+b的解析式;
(2)将直线y=kx+b平移,若它与矩形有公共点,直接写出b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣2的图象与x轴交于A,B两点,与y轴交于点C,点A的坐标为(4,0),且当x=﹣2和x=5时二次函数的函数值y相等.
(1)求实数a、b的值;
(2)如图1,动点E,F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒 ![]() 个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由.
②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个自色六边形相邻,若一段边框上有25个黑色六边形,则这段边框共有白色六边形

A. 100个 B. 102个 C. 98个 D. 150个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com