
【题目】如图,点C是∠ABC一边上一点 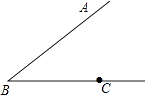
(1)按下列要求进行尺规作图: ①作线段BC的中垂线DE,E为垂足.
②作∠ABC的平分线BD.
③连结CD,并延长交BA于F.
(2)若∠ABC=62°,求∠BFC的度数.
【答案】
(1)解:答案如图所示.
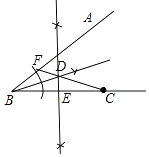
(2)解:∵∠ABC=62°,BD为∠ABC的平分线
∴∠ABD=∠CBD=31°
∵DE是BC的中垂线
∴BD=CD
∴∠CBD=∠DCB=31°
∴∠BFC=180°﹣∠FBC﹣∠FCB=180°﹣62°﹣31°=87°
【解析】(1)根据线段垂直平分线的画法.角平分线的画法,画出图形即可.(2)根据∠BFC=180°﹣∠FBC﹣∠FCB,求出∠FCB即可.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】⊙O的半径为5,点A与圆心O的距离为OA=4,则点A与⊙O的位置关系为( )
A.点A在⊙O内B.点A在⊙O上
C.点A在⊙O外D.以上三种情况都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E. 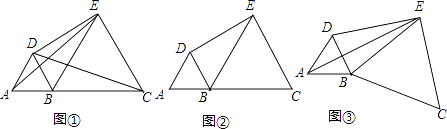
(1)如图①,连结CD,AE,求证:CD=AE;
(2)如图②,若AB=1,BC=2,求DE的长;
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2 , 试求∠DEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的 顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,a=![]() .其中正确的是( )
.其中正确的是( )
A. ②④ B. ②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各项目的工作量如图所示:
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为________,每人每分钟擦课桌椅________m2;
(2)扫地拖地的面积是________m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?(要有详细的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司的甲、乙两辆货车分别从相距300千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车行驶1.5小时时甲车先到达配货站C地,此时两车相距30千米,甲车在C地用1小时配货,然后按原速度开往B地;乙车行驶2小时时也到C地,未停留继续开往A地。(友情提醒:画出线段图帮助分析)
(1)乙车的速度是 千米/小时,B、C两地的距离是 千米,A、C两地的距离是 千米;
(2)求甲车的速度及甲车到达B地所用的时间;
(3)乙车出发多长时间,两车相距150千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算错误的是( )
A. a2÷a0a2=a4 B. a2÷(a0a2)=1
C. (﹣1.5)8÷(﹣1.5)7=﹣1.5 D. ﹣1.58÷(﹣1.5)7=﹣1.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com