
【题目】在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E. 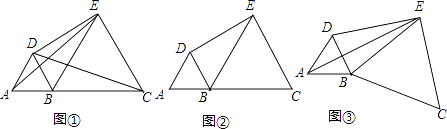
(1)如图①,连结CD,AE,求证:CD=AE;
(2)如图②,若AB=1,BC=2,求DE的长;
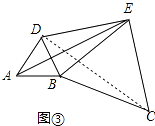
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2 , 试求∠DEB的度数.
【答案】
(1)证明:如图①中,∵△ABD和△ECB都是等边三角形,
∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,
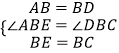 ,
,
∴△ABE≌△DBC,
∴AE=DC.
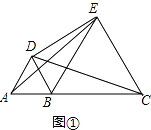
(2)解:如图②中,取BE中点F,连接DF.
∵BD=AB=1,BE=BC=2,∠ABD=∠EBC=60°,
∴BF=EF=1=BD,∠DBF=60°,
∴△DBF是等边三角形,
∴DF=BF=EF,∠DFB=60°,
∵∠BFD=∠FED+∠FDE,
∴∠FDE=∠FED=30°
∴∠EDB=180°﹣DEB∠DBE﹣∠DEB=90°,
∴DE= ![]() =
= ![]() =
= ![]() .
.
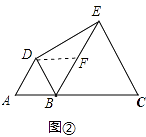
(3)解:如图③中,连接DC,
∵△ABD和△ECB都是等边三角形,
∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,
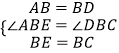 ,
,
∴△ABE≌△DBC,
∴AE=DC.
∵DE2+BE2=AE2,BE=CE,
∴DE2+CE2=CD2,
∴∠DEC=90°,
∵∠BEC=60°,
∴∠DEB=∠DEC﹣∠BEC=30°.
【解析】(1)欲证明CD=AE,只要证明△ABE≌△DBC即可.(2)如图②中,取BE中点F,连接DF,首先证明△BDE是直角三角形,再利用勾股定理即可.(3)如图③中,连接DC,先利用勾股定理的逆定理证明△DEC是直角三角形,得∠DEC=90°即可解决问题.


科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.矩形的对角线互相垂直
C.菱形的对角线互相垂直且平分
D.对角线互相垂直,且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在绣湖公园的A处正面观测解百购物中心墙面上的电子屏幕,测得屏幕上端C处的仰角为30°,接着他正对电子屏幕方向前进7m到达B处,又测得该屏幕上端C处的仰角为45°.已知电子屏幕的下端离开地面距离DE为4m,小杨的眼睛离地面1.60m,电子屏幕的上端与墙体的顶端平齐.求电子屏幕上端与下端之间的距离CD(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是∠ABC一边上一点 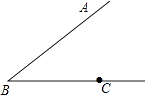
(1)按下列要求进行尺规作图: ①作线段BC的中垂线DE,E为垂足.
②作∠ABC的平分线BD.
③连结CD,并延长交BA于F.
(2)若∠ABC=62°,求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知A(﹣1,2),B(﹣3,1)C(0,﹣1)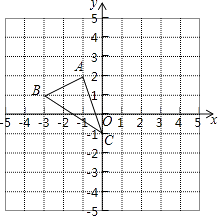
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1
(2)若将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 .
(3)AC的长等于 , △ABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用三个正多边形镶嵌成一个平面时,若前两种是正方形和正六边形,则第三种是( )
A. 正十二边形 B. 正十边形 C. 正八边形 D. 正三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com