
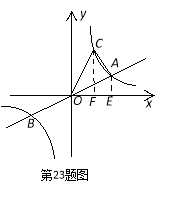
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线
交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线![]() 上一点,且点C在直线
上一点,且点C在直线![]() 的上方.
的上方.
(1)求双曲线的函数解析式;(2)若△AOC的面积为6,求点C的坐标.

【答案】(1)![]() (2)(2,4)
(2)(2,4)
【解析】
试题分析:(1)把点B的坐标代入反比例函数解析式求出k值,
(2)再根据反比例函数图象的中心对称性求出点A的坐标,然后过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为(a, ![]() ),然后根据
),然后根据![]() 列出方程求解即可得到a的值,从而得解.
列出方程求解即可得到a的值,从而得解.
试题解析:(1)∵点B(﹣4,﹣2)在双曲线![]() 上,
上,
∴![]() ,∴k=8,
,∴k=8,
∴双曲线的函数解析式为![]()
(2)过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,
∵正比例函数与反比例函数的交点A、B关于原点对称,
∴A(4,2),∴OE=4,AE=2,
设点C的坐标为(![]() ,
,![]() ),则OF=
),则OF=![]() ,CF=
,CF=![]() ,
,
则![]()
![]()
![]()
∵△AOC的面积为6,∴![]() ,
,
整理得,![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴点C的坐标为(2,4).


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
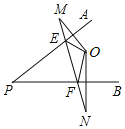
【题目】如图,已知点O是∠APB内的一点,M,N分别是点O关于PA、PB的对称点,连接MN,与PA、PB分别相交于点E、F,已知MN=6cm.
(1)求△OEF的周长;
(2)连接PM、PN,若∠APB=ɑ,求∠MPN(用含ɑ的代数式表示);
(3)当∠ɑ=30°,判定△PMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海世博会会期为2010年5月1日至2010年10月31日。门票设个人票和团队票两大类。个人普通票160元/张,学生优惠票100元/张;成人团队票120元/张,学生团队票50元/张。
(1)如果2名老师、10名学生均购买个人票去参观世博会,请问一共要花多少元钱购买门票?
(2)用方程组解决下列问题:如果某校共30名师生去参观世博会,并得知他们都是以团队形式购买门票,累计花去2200元,请问该校本次分别有多少名老师、多少名学生参观世博会?
查看答案和解析>>
科目:初中数学 来源: 题型:
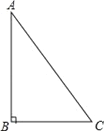
【题目】已知Rt△ABC中,∠B=90°,
(1)根据要求作图(尺规作图,保留作图痕迹,不写画法):
①作∠BAC的平分线AD交BC于D;
②作线段AD的垂直平分线交AB于E,交AC于F,垂足为H;
③连接ED.
(2)在(1)的基础上写出一对全等三角形:△ ≌△ 并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com