
【题目】(本小题满分9分)已知点D是![]() 边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
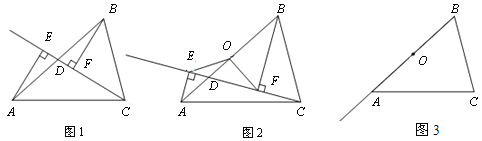
(1)如图1,当点D与点O重合时,AE与BF的位置关系是____________,OE与OF的数量关系是__________;
(2)如图2,当点D在线段AB上不与点O重合时,试判断OE与OF的数量关系,并给予证明;
(3)如图3,当点D在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.
【答案】(1)AE∥BF,OE=OF;(2) OE=OF,证明见解析;(3)(2)中的结论成立,图形及证明思路见解析.
【解析】(1)AE∥BF,OE=OF.
如图,
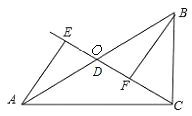
当点D与点O重合时,AE与BF的位置关系是AE∥BF,OE与OF的数量关系是OE=OF.
理由是:∵O为AB的中点,
∴AO=BO,
∵AE⊥CD,BF⊥CO,
∴AE∥BF,∠AEO=∠BFO=90°,(2分)
在![]() 和
和![]() 中
中
∠AOE=∠BOF,∠AEO=∠BFO,AO=BO,
∴△AEO≌△BFO,
∴OE=OF,
故答案为:AE∥BF,OE=OF(3分)
(2)结论:OE=OF. (4分)
证明:如图,延长EO交BF于G.

∵AE∥BF,
∴∠AEO=∠BGO,
在![]() 和
和![]() 中,
中,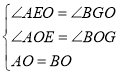 ,
,
∴△AEO≌△BGO(ASA).
∴OE=OG.
∵BF⊥CD,
∴FO是![]() 斜边上的中线,
斜边上的中线,
∴OE=OF=OG,
即OE=OF.(6分)
(3)(2)中的结论仍然成立. (7分)
所画图形如图所示,
 (8分)
(8分)
证明思路:延长EO、FB交于G.
由(2)的证明思路可以得到△AOE≌△BOG,由全等得到OE=OG;由BF⊥CD,得到FO是![]() 斜边GE上的中线;可得到OE=OF.(9分)
斜边GE上的中线;可得到OE=OF.(9分)


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】莆田市政府推出“Youbike微笑自行车”的社会公共服务项目,旨在发展全民健身打造健康莆田,预计2019年年底将建设970个公共自行车租赁站点,投入自行车31000辆.将31000写成科学记数法为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车队运送一批救灾物资,若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,恰好装完.设这个车队有x辆车,则( )
A.4(x+8)=4.5xB.4x+8=4.5xC.4.5(x-8)=4xD.4x+4.5x=8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人的大脑所能记忆的内容是有限的,随着时间的推移,记忆的东西会逐渐遗忘.为提升记忆的效果,需要有计划的按时复习巩固.图中的实线部分是记忆保持量(%)与时间(天)之间的关系图.请根据图回答下列问题: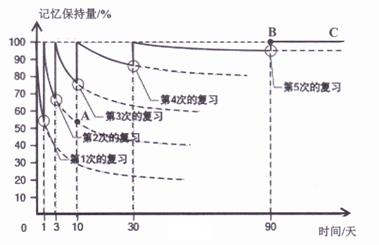
(1)图中的自变量是 , 应变量是;
(2)如果不复习,3天后记忆保持量约为;
(3)图中点A表示的意义是;
(4)图中射线BC表示的意义是;
(5)经过第1次复习与不进行复习,3天后记忆保持量相差约为;
(6)10天后,经过第2次复习与从来都没有复习的记忆保持量相差约为.
查看答案和解析>>
科目:初中数学 来源: 题型:
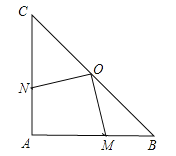
【题目】(本小题满分9分)如图,在![]() 中,∠A=90°,AB=AC=4 cm,若O是BC的中点,动点M在AB上移动,动点N在AC上移动,且AN=BM .
中,∠A=90°,AB=AC=4 cm,若O是BC的中点,动点M在AB上移动,动点N在AC上移动,且AN=BM .
(1)证明:OM = ON;
(2)在点M,N运动的过程中,四边形AMON的面积是否发生变化,若发生变化,请说明理由;若不变,请你求出四边形AMON的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com