
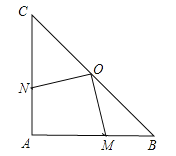
【题目】(本小题满分9分)如图,在![]() 中,∠A=90°,AB=AC=4 cm,若O是BC的中点,动点M在AB上移动,动点N在AC上移动,且AN=BM .
中,∠A=90°,AB=AC=4 cm,若O是BC的中点,动点M在AB上移动,动点N在AC上移动,且AN=BM .
(1)证明:OM = ON;
(2)在点M,N运动的过程中,四边形AMON的面积是否发生变化,若发生变化,请说明理由;若不变,请你求出四边形AMON的面积.
【答案】见解析
【解析】(1)连接OA(如图).
∵在Rt![]() ABC中,AB=AC,∴
ABC中,AB=AC,∴![]() ABC是等腰直角三角形,
ABC是等腰直角三角形,
∴∠ABC=45°,即∠ABO=45°.(2分)
∵O是BC的中点,且![]() ABC是等腰直角三角形,
ABC是等腰直角三角形,
∴AO⊥BC,
∴在![]() AOB中,∠OAB=90°∠ABO=90°45°=45°,
AOB中,∠OAB=90°∠ABO=90°45°=45°,
∴∠OAB=∠ABO,
∴OA=OB,
∵O是BC的中点,且![]() 是等腰直角三角形,∠BAC=90°,
是等腰直角三角形,∠BAC=90°,
∴![]() ,
,
∴∠OAC=∠ABO=45°,即∠OAN=∠OBM,(3分)
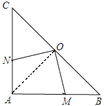
∵在![]() 与
与![]() 中
中
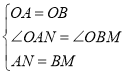 ,
,
∴![]() ,
,
∴ON=OM,即OM=ON.(5分)
(2)在动点M、N运动的过程中,四边形AMON的面积不变.(6分)
理由如下:
连接OA.
由第(1)小题的证明可知:![]() ,
,
∴△OAN的面积等于![]() 的面积,
的面积,
∵四边形AMON的面积等于![]() 的面积与
的面积与![]() 的面积之和,
的面积之和,
∴四边形AMON的面积等于![]() 的面积与
的面积与![]() 的面积之和,
的面积之和,
∵![]() 的面积与
的面积与![]() 的面积之和等于
的面积之和等于![]() 的面积,
的面积,
∴四边形AMON的面积等于![]() 的面积,
的面积,
∵O是BC的中点,且![]() 是等腰直角三角形,
是等腰直角三角形,
∴△![]() 的面积的一半,(7分)
的面积的一半,(7分)
∵AB=AC=4 cm,
∴![]() 的面积为
的面积为![]() (cm2),
(cm2),
∴△OAB的面积为:![]() (cm2),
(cm2),
∴四边形AMON的面积为4 cm2.(9分)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2018年10月24日上午9时港珠澳大桥正式通车,它是东亚建设的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,整个大桥造价超过720亿元人民币,将72000000000用科学记数法表示为( )
A.7.2×1011B.7.2×1010C.0.72×1011D.72×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某函数满足当自变量x=-1时,函数的值y=2,且函数y的值始终随自变量x的增大而减小,写出一个满足条件的函数表达式____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)已知点D是![]() 边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
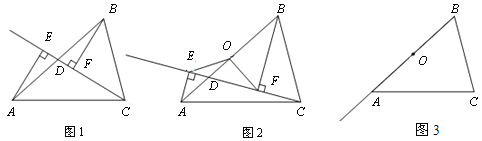
(1)如图1,当点D与点O重合时,AE与BF的位置关系是____________,OE与OF的数量关系是__________;
(2)如图2,当点D在线段AB上不与点O重合时,试判断OE与OF的数量关系,并给予证明;
(3)如图3,当点D在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=x2+2y2﹣z,B=﹣4x2+3y2+2z,且A+B+C=0,则多项式C为( )
A. 5x2﹣y2﹣z B. x2﹣y2﹣z C. 3x2﹣y2﹣3z D. 3x2﹣5y2﹣z
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com