
【题目】已知AB=10cm,点C在直线AB上,如果BC=4cm,点D是线段AC的中点,求线段BD的长度.
【答案】解:∵AB=10cm,BC=4cm,点C在直线AB上, ∴点C在线段AB上或在线段AB的延长线上.
①当点C在线段AB上时,如图①,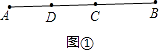
则有AC=AB﹣BC=10﹣4=6.
∵点D是线段AC的中点,
∴DC= ![]() AC=3,
AC=3,
∴DB=DC+BC=3+4=7;
②当点C在线段AB的延长线上时,如图②,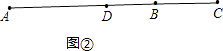
则有AC=AB+BC=10+4=14.
∵点D是线段AC的中点,
∴DC= ![]() AC=7,
AC=7,
∴DB=DC﹣BC=7﹣4=3.
综上所述:线段BD的长度为7cm或3cm.
【解析】由于AB>BC,点C在直线AB上,因此可分点C在线段AB上、点C在线段AB的延长线上两种情况讨论,只需把BD转化为DC与BC的和或差,就可解决问题.
【考点精析】认真审题,首先需要了解两点间的距离(同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分9分)已知点D是![]() 边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
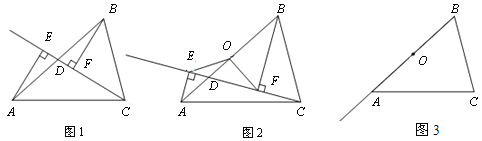
(1)如图1,当点D与点O重合时,AE与BF的位置关系是____________,OE与OF的数量关系是__________;
(2)如图2,当点D在线段AB上不与点O重合时,试判断OE与OF的数量关系,并给予证明;
(3)如图3,当点D在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
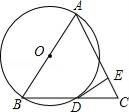
【题目】如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.
证明:(1)BD=DC;(2)DE是⊙O切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
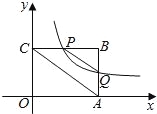
【题目】如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线![]() (x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
(1)若P为边BC的中点,求双曲线的函数表达式及点Q的坐标;
(2)求k的取值范围;
(3)连接PQ,AC,判断:PQ∥AC是否总成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个箱子中放有红、黄、黑三种只有颜色不同的小球,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢,这个游戏是( )
A. 公平的
B. 不公平的
C. 先摸者赢的可能性大
D. 后摸者赢的可能性大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com