
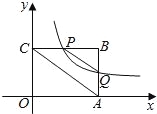
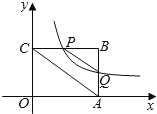
【题目】如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线![]() (x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
(1)若P为边BC的中点,求双曲线的函数表达式及点Q的坐标;
(2)求k的取值范围;
(3)连接PQ,AC,判断:PQ∥AC是否总成立?并说明理由.
【答案】(1)y=![]() ,(4,
,(4,![]() )(2)0<k<12(3)PQ∥AC总成立
)(2)0<k<12(3)PQ∥AC总成立
【解析】
试题分析:(1)先求出点P坐标,再利用待定系数法求出反比例函数解析式,根据点Q的横坐标即可求出点Q的纵坐标.
(2)设点P(x,3),则x=![]() ,列出不等式即可解决问题.
,列出不等式即可解决问题.
(3)根据两边成比例夹角相等的两个三角形相似证明△BPQ∽△BCA,即可解决问题.
试题解析:(1)∵四边形OABC是矩形,
∴BC∥OA,
∵点B坐标(4,3),
∴BC=4,AB=3,
∵PC=PB,
∴点P坐标(2,3),
∴反比例函数解析式y=![]() ,
,
∵点Q的横坐标为4,
∴点Q的坐标为(4,![]() ).
).
(2)设点P坐标(x,3),则0<x<4,
把点P(x,3)代入y=![]() 得到,x=
得到,x=![]() ,
,
∴0<![]() <4,
<4,
∴0<k<12.
(3)结论:PQ∥AC总成立.
理由:设P(m,3),Q(4,n),则3m=4n=k,
∴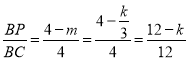 ,
,
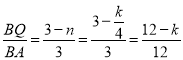 ,
,
∴![]() ,
,
∵∠B=∠B,
∴△BPQ∽△BCA,
∴∠BPQ=∠BCA,
∴PQ∥AC.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】人的大脑所能记忆的内容是有限的,随着时间的推移,记忆的东西会逐渐遗忘.为提升记忆的效果,需要有计划的按时复习巩固.图中的实线部分是记忆保持量(%)与时间(天)之间的关系图.请根据图回答下列问题: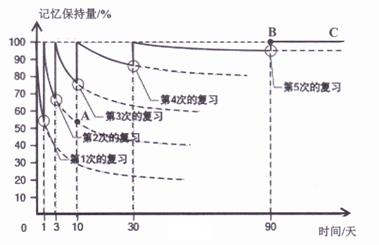
(1)图中的自变量是 , 应变量是;
(2)如果不复习,3天后记忆保持量约为;
(3)图中点A表示的意义是;
(4)图中射线BC表示的意义是;
(5)经过第1次复习与不进行复习,3天后记忆保持量相差约为;
(6)10天后,经过第2次复习与从来都没有复习的记忆保持量相差约为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )
A.0.25×10﹣5
B.0.25×10﹣6
C.2.5×10﹣5
D.2.5×10﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
学习完本册第二章“轴对称图形”后,张老师在课堂上提出这样的问题:“如图①,在△ABC中,∠A=30°,∠B=60°,如何画一条线段把△ABC分割成两个等腰三角形?”请在图中画出这条线段,并标出相关的度数.
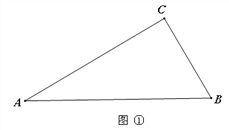
问题探究
探究一:课后,小华经过探究发现:如图②,在△ABC中,∠A=26°,∠B=52°,也可以画一条线段把△ABC分割成两个等腰三角形.请在图中画出这条线段,并标出相关的度数.
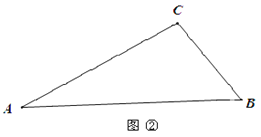
探究二:如图③,在△ABC中,当,∠B=2∠A时,是否一定存在一条线段把△ABC分割成两个等腰三角形?若能,请在图中画出这条线段,若不能,直接写出∠A的取值范围.
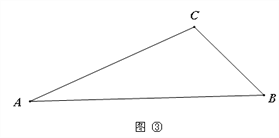
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com