练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，折叠矩形纸片ABCD，先折出折痕（对角线）BD，再折叠AD边与对角线BD重合，得折痕DG，如图所示，若AB=8，BC=6，求AG的长．

    3．

    【解析】

    试题分析：根据勾股定理可得BD=10，由折叠的性质可得△ADG≌△A1DG，则A1D=AD=6，A1G=AG，则A1B=10-6=4，在Rt△A1BG中根据勾股定理求AG的即可．

    试题解析：如图

    在Rt△ABD中，AB=8，AD=6，

    则BD=，

    由折叠的性质可得：△ADG≌△A1DG，

    ∴A1D=AD=6，A1G=AG，

    ∴A1B=10-6=4，

    设AG=x，则：A1G=AG=x，BG=8-x，

    在Rt△A1BG中，x2+42=（8-x）2

    解得：x=3，

    即AG长为3．

    考点：翻折变换（折叠问题）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    声音在空气中每小时约传播1200千米，将1200用科学记数法表示为　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


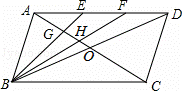
     如图，在▱ABCD中，对角线AC、BD相交于点O，点E、F是AD上的点，且AE=EF=FD．连接BE、BF，使它们分别与AO相交于点G、H．

    （1）求EG：BG的值；

    （2）求证：AG=OG；

    （3）设AG=a，GH=b，HO=c，求a：b：c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     计算：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点P是正方形ABCD内一点，点P到点A，B和D的距离分别为1，，．△ADP沿点A旋转至△ABP’，连结PP’，并延长AP与BC相交于点Q．

    （1）求证：△APP’是等腰直角三角形；

    （2）求∠BPQ的大小；

    （3）求CQ的长．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年陕西省西安市八年级下学期第一次月考数学试卷（解析版） 题型：填空题

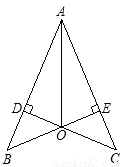
    如图，已知CD⊥AD，BE⊥AC，垂足为D、E，BE、CD交于点O，且AO平分∠BAC，那么图中共有全等三角形 对．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年陕西省西安市八年级下学期第一次月考数学试卷（解析版） 题型：选择题

    如图，△ABC中，已知∠B和∠C的平分线相交于点F，经过点F作DE//BC，交AB于D，交AC于点E，若BD+CE=9，则线段DE的长为（ ）

    A、9 B、8 C、7 D、6

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年江苏省东台第一教研片七年级下学期第一次月考数学卷（解析版） 题型：选择题

    若两条平行线被第三条直线所截，则一组同旁内角的平分线（ ）．

    A．互相垂直 B．互相平行 C．互相重合 D．关系不确定

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年湖南省衡阳市七年级上学期期末考试数学试卷（解析版） 题型：解答题

    如图，点O为直线AB上一点，过点O作射线OC，使∠BOC=120°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．

    （1）将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC．问：此时直线ON是否平分∠AOC？请说明理由．

    （2）将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为 （直接写出结果）．

    （3）将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，求∠AOM -∠NOC的度数．

    查看答案和解析>>

    同步练习册答案