
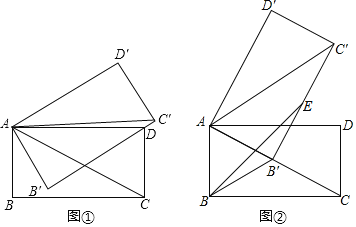
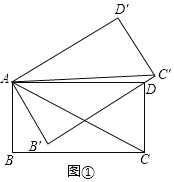
【题目】在矩形ABCD中,AB=2,∠ACB=30°,将矩形ABCD绕点A逆时针方向旋转,得到矩形AB′C′D′,记旋转角为α(0<α<90°).
(I)如图①,当B'C'过点D时,求△ADC'的面积S的值;
(Ⅱ)如图②,当点B的对应点B'落在AC上时,在B′C′上取点E,使B'E=AB.
①求∠EBB'的大小;
②求BE的长(直接写出结果即可).
【答案】(Ⅰ)S△ADC′=2![]() ﹣2
﹣2![]() ;(Ⅱ)①∠BEB′=15°;②BE=
;(Ⅱ)①∠BEB′=15°;②BE=![]()
![]() .
.
【解析】
(Ⅰ)如图①中,解直角三角形求出DB′,根据S△ADC′=S△AB′C′﹣S△ADB′,计算即可.
(Ⅱ)①证明△ABB′是等边三角形,利用圆周角定理即可解决问题.
②如图②中,作EH⊥BB′交BB′于H.解直角三角形求出EH,BH,利用勾股定理即可解决问题.
解:(Ⅰ)如图①中,
在Rt△ABC中,∵∠B=90°,AB=2,∠ACB=30°,
∴AC=2AB=4,![]() ,
,
在Rt△ADB′中,![]() ,
,
∴![]()
(Ⅱ)①如图②中,连接AE.
∵AB=AB′,∠BAB′=60°,
∴△ABB′是等边三角形,
∴B′A=B′B=B′E,∠AB′B=60°,
∴点B′是△ABE的外接圆的圆心,
∴![]() ,
,
∵∠AB′E=90°,B′A=B′E,
∴∠AEB′=45°,
∴∠BEB′=45°﹣30°=15°.
②如图②中,作EH⊥BB′交BB′于H.
∵B′E=B′B,
∴∠B′BE=∠B′EB=15°,
∴∠EB′H=30°,
∴EH=![]() EB′=1,HB′=
EB′=1,HB′=![]() ,
,
∴![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
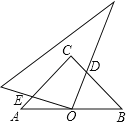
【题目】如图,在Rt△ABC中,∠C=90°.点O是AB的中点,边AC=6,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点0旋转,始终保持三角板的直角边与AC相交,交点为点E,另条直角边与BC相交,交点为D,则等腰直角三角板的直角边被三角板覆盖部分的两条线段CD与CE的长度之和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:
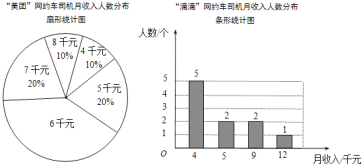
根据以上信息,整理分析数据如下:

(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣x﹣6.
(1)画出函数的图象;
(2)观察图象,指出方程x2﹣x﹣6=0的解及不等式x2﹣x﹣6>0解集;
(3)求二次函数的图象与坐标轴的交点所构成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中∠ACB=90°、∠CAB=30°,△ABD 是等边三角形将四边形 ACBD 折叠,使点 D 与点 C 重合,HK 为折痕,则cos∠ACH 的值是( )
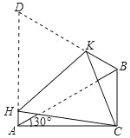
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() 、交
、交![]() 轴于点
轴于点![]() ,
,
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)设点![]() 是
是![]() 轴上的一点
轴上的一点
①在坐标平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,求出
为顶点的四边形是菱形?若存在,求出![]() 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
②若![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 在直线
在直线![]() 上,当
上,当![]() 为等边三角形时,求直线
为等边三角形时,求直线![]() 的函数表达式.
的函数表达式.
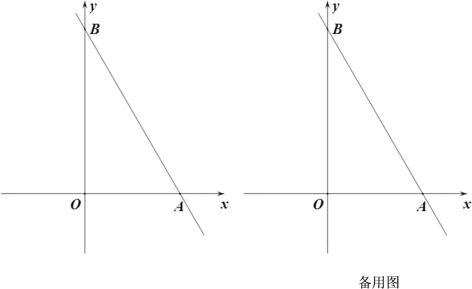
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com