
【题目】如图,在平面直角坐标系xOy中,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() 、交
、交![]() 轴于点
轴于点![]() ,
,
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)设点![]() 是
是![]() 轴上的一点
轴上的一点
①在坐标平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,求出
为顶点的四边形是菱形?若存在,求出![]() 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
②若![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 在直线
在直线![]() 上,当
上,当![]() 为等边三角形时,求直线
为等边三角形时,求直线![]() 的函数表达式.
的函数表达式.
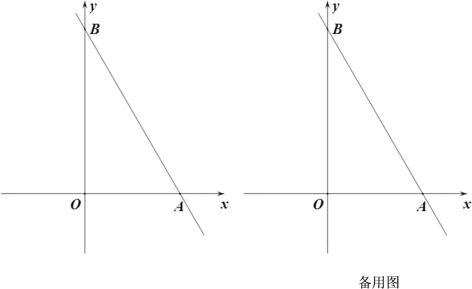
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,
, ![]()
![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)将点A的坐标代入直线![]() :
:![]() 中即可求出直线的解析式;
中即可求出直线的解析式;
(2)①先假设存在点Q,则以A,P,B,Q为顶点的四边形是菱形,再利用菱形的性质求点Q的坐标即可,如果能求出来,说明存在,反之则不存在;
②要求DM的直线必须知道点M的坐标,求点M的坐标必须把它放到直角三角形中去求.利用关于y轴对称的点的特点和等边三角形的性质,结合全等三角形及锐角三角函数解题即可.
解:(1)将![]() 代入
代入![]() 得,
得,
![]() ,
,
解得![]()
所以,直线![]() 的函数表达式为
的函数表达式为![]() ;
;
(2)①直线l中,令x=0,y=![]() ,∴OB=
,∴OB=![]()
由勾股定理得![]()
若AP为对角线时,有两种情况:
∵BP∥AQ
∴Q点与A点横坐标相同
∵四边形ABPQ是菱形
∴AQ=AB=8
若点P在点B上端,则Q的坐标为(4,8)
若点P在点B下端,则Q的坐标为(4,-8)
若AB为对角线
∵四边形APBQ为菱形
设AB,PQ交于点D
∴AB⊥PQ,![]()
∴tan∠OBA=![]()
∴∠OBA=30°
∵PB∥AQ
∴∠BAQ=30°
在Rt△ADQ中,![]()
∴![]()
∴Q的坐标为![]()
若BP为对角线
∵四边形ABQP为菱形
∴BP⊥AQ,AO=OQ
∴Q的坐标为![]()
综上所述,这样的Q点有4个,分别是
![]() ,
,![]() ,
, ![]()
![]()
②点D与C点关于y轴对称,所以D的坐标为(-2,0)
如图,当点![]() 在
在![]() 轴上方时,
轴上方时,
将![]() 及CD边绕点
及CD边绕点![]() 逆时针旋转至点
逆时针旋转至点![]() 与点
与点![]() 重合,设
重合,设![]() 与
与![]() 重合,则
重合,则![]() ,
,![]() ,作MQ⊥AD于点Q
,作MQ⊥AD于点Q
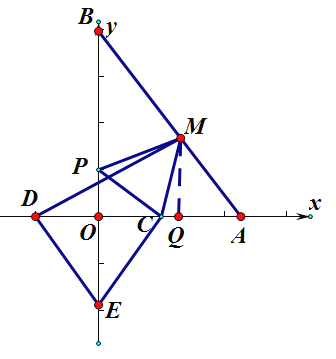
∵CD=CE, ![]()
∴![]() 为等边三角形
为等边三角形
∴点![]() 在
在![]() 的中垂线上,即在
的中垂线上,即在![]() 轴上,于是
轴上,于是![]()
∵∠MCP=∠DCE=60°
∴∠MCP+∠PCD=∠DCE+∠PCD
∴∠MCD=∠PCE
在△MCD和△PCE中
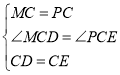
∴△MCD≌△PCE(SAS)
∴![]()
在Rt△AMQ中,
∵∠BAO=60°
∴tan60°=![]()
设AQ=x,则MQ=![]()
在Rt△DMQ中,
![]()
解得![]()
∴![]()
∴![]()
设DM的直线方程为![]()
将D(-2,0),![]() 代入直线方程中
代入直线方程中
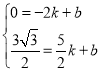 解得
解得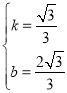
所以,直线DM的函数表达式为 ![]()
当点![]() 在
在![]() 轴下方时,同理可得直线
轴下方时,同理可得直线![]() 的函数表达式为
的函数表达式为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
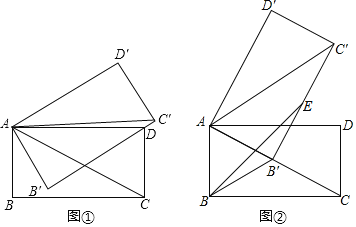
【题目】在矩形ABCD中,AB=2,∠ACB=30°,将矩形ABCD绕点A逆时针方向旋转,得到矩形AB′C′D′,记旋转角为α(0<α<90°).
(I)如图①,当B'C'过点D时,求△ADC'的面积S的值;
(Ⅱ)如图②,当点B的对应点B'落在AC上时,在B′C′上取点E,使B'E=AB.
①求∠EBB'的大小;
②求BE的长(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
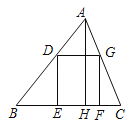
【题目】如图,四边形DEFG是△ABC的内接正方形,D、G分别在AB、AC上,E、F在BC上,AH是△ABC的高,已知BC=20,AH=16,求正方形DEFG的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
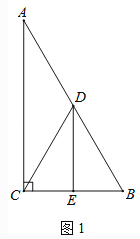
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
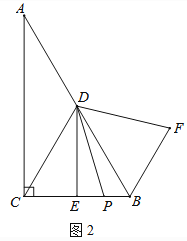
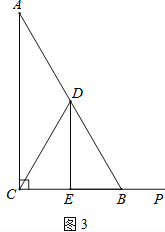
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙、丙三人组成的篮球训练小组,他们三人之间进行互相传球练习,篮球从一个人手中随机传到另外一个人手中计作传球一次,共连续传球三次.
(1)若开始时篮球在甲手中,则经过第一次传球后,篮球落在丙的手中的概率是 ;
(2)若开始时篮球在甲手中,求经过连续三次传球后,篮球传到乙的手中的概率.(请用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,解一元二次方程,可以把它转化为两个一元一次方程来解,其实用“转化”的数学思想我们还可以解一些新的方程例如一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,通过解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.
(1)方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)用“转化”的思想求方程![]() =x的解.
=x的解.
(3)试直接写出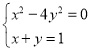 的解 .
的解 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班学生做“用频率估计概率”的实验时,给出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )
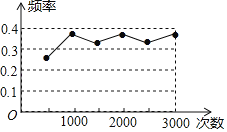
A.抛一枚硬币,出现正面朝上
B.从标有1,2,3,4,5,6的六张卡片中任抽一张,出现偶数
C.从一个装有6个红球和3个黑球的袋子中任取一球,取到的是黑球
D.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com