
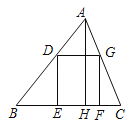
【题目】如图,四边形DEFG是△ABC的内接正方形,D、G分别在AB、AC上,E、F在BC上,AH是△ABC的高,已知BC=20,AH=16,求正方形DEFG的边长.
科目:初中数学 来源: 题型:
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
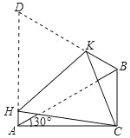
【题目】如图,在△ABC 中∠ACB=90°、∠CAB=30°,△ABD 是等边三角形将四边形 ACBD 折叠,使点 D 与点 C 重合,HK 为折痕,则cos∠ACH 的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
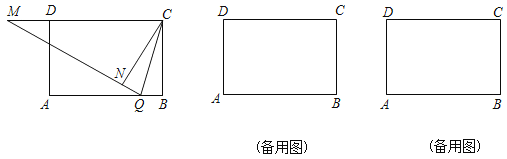
【题目】如图,在矩形ABCD中,AB=6,BC=4,动点Q在边AB上,连接CQ,将△BQC沿CQ所在的直线对折得到△CQN,延长QN交直线CD于点M.
(1)求证:MC=MQ
(2)当BQ=1时,求DM的长;
(3)过点D作DE⊥CQ,垂足为点E,直线QN与直线DE交于点F,且![]() ,求BQ的长.
,求BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,2),抛物线y=mx2+4mx+5m的对称轴与x轴交于点B.
(1)求点B的坐标;
(2)当m>0时,过A点作直线l平行于x轴,与抛物线交于C、D两点(C在D左侧),C、D横坐标分别为x1、x2,且x2﹣x1=2,求抛物线的解析式;
(3)若抛物线与线段AB恰只有一个公共点,则请结合函数图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
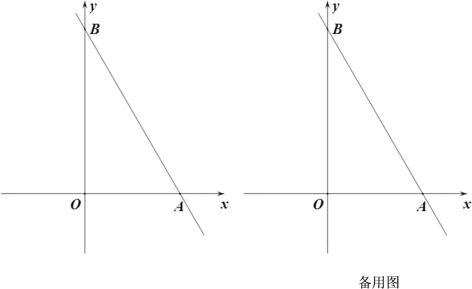
【题目】如图,在平面直角坐标系xOy中,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() 、交
、交![]() 轴于点
轴于点![]() ,
,
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)设点![]() 是
是![]() 轴上的一点
轴上的一点
①在坐标平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,求出
为顶点的四边形是菱形?若存在,求出![]() 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
②若![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 在直线
在直线![]() 上,当
上,当![]() 为等边三角形时,求直线
为等边三角形时,求直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com