
【题目】如图,∠AOB=90°,在∠AOB的内部有一条射线OC.
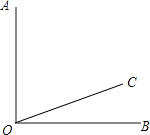
(1)画射线OD⊥OC.
(2)写出此时∠AOD与∠BOC的数量关系,并说明理由.
科目:初中数学 来源: 题型:
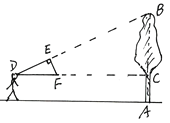
【题目】如图,小明用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m, CD=10 m,请你帮小明求下树的高度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
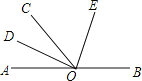
(1)若∠AOC=50°,求出∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
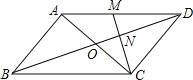
(1)求BD的长;
(2)在直线AC的同侧,以点O为位似中心,作出△CON的位似三角形,并使△CON与和它位似的三角形的位似比是1:2.(写出结果,不写作法,保留作图痕迹).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com