
【题目】如图,在平面直角坐标系中,已知点P(5,5),点B、A分别在x轴、y轴正半轴上,且∠APB=90°,则OA+OB= .
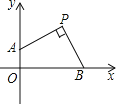
【答案】10
【解析】
试题分析:过P作PM⊥y轴于M,PN⊥x轴于N,得出四边形PMON是正方形,推出OM=ON=PN=3,证△APM≌△BPN,推出AM=BN,求出OA+OB=ON+OM,代入求出即可.
解:过P作PM⊥y轴于M,PN⊥x轴于N,
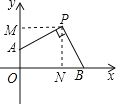
∵P(5,5),
∴PN=PM=5,
∵x轴⊥y轴,
∴∠MON=∠PNO=∠PMO=90°,
∴∠MPN=360°﹣90°﹣90°﹣90°=90°,
则四边形MONP是正方形,
∴OM=ON=PN=PM=5,
∵∠APB=90°,
∴∠APB=∠MON,
∴∠MPA=90°﹣∠APN,∠BPN=90°﹣∠APN,
∴∠APM=∠BPN,
在△APM和△BPN中,
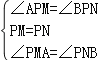 ,
,
∴△APM≌△BPN(ASA),
∴AM=BN,
∴OA+OB
=OA+0N+BN
=OA+ON+AM
=ON+OM
=5+5
=10.
故答案为:10.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.
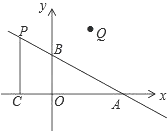
(1)当b=3时,
①求直线AB的解析式;
②若QO=QA,求P点的坐标.
(2)是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是( )
A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍。乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠。该班需球拍5副,乒乓球若干盒(不小于5盒)。
问:(1)设购买乒乓球x盒时,在甲家购买所需多少元?在乙家购买所需多少元?(用含x的代数式表示,并化简)(4分)
(2)当购买乒乓球多少盒时,两种优惠办法付款一样?(2分)
(3)当购买30盒乒乓球时,若让你选择一家商店去办这件事,你打算去哪家商店购买?为什么?(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①负数没有立方根,②一个实数的立方根不是正数就是负数,③一个正数或负数的立方根与这个数的符号一致,④如果一个数的立方根等于它本身,那么它一定是1或0.其中正确的是( )
A、1 B、2 C、3 D、4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个布袋中装有2个红球和2个篮球,它们除颜色外其他都相同.
(1)搅匀后从中摸出一个球记下颜色,不放回继续再摸第二个球,求两次都摸到红球的概率;
(2)在这4个球中加入x个用一颜色的红球或篮球后,进行如下试验,搅匀后随机摸出1个球记下颜色,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到红球的概率稳定在0.80,请推算加入的是哪种颜色的球以及x的值大约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com