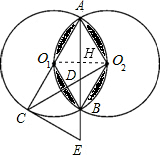考点:圆的综合题,勾股定理,菱形的判定与性质,切线的性质,扇形面积的计算,相似三角形的判定
专题:综合题
分析:(1)由⊙O1和⊙O2是等圆即可推出四边形AO1BO2是菱形.
(2)易证△AO1O2和△BO1O2都是等边三角形,从而有∠AO2B=∠AO1B=120°,而AB左右两阴影部分面积相等,左部分的面积等于S扇形O2AB-S菱形AO1BO2,根据扇形和菱形的面积公式就可求出图中阴影部分的面积.
(3)易证∠AO2D=∠ACE=90°,∠O2AD=∠CAE,从而有△AO2D∽△ACE,且相似比为AO2:AC=1:2.
解答:解:(1)证明:∵⊙O
1和⊙O
2是等圆
∴AO
1=BO
1=O
2A=O
2B,
∴四边形AO
1BO
2是菱形.
(2)连接O
1O
2,交AB于点H,如图所示,
∵四边形AO
1BO
2是菱形,
∴AB⊥O
1O
2,AH=BH,O
1H=O
2H=1.
∵O
1A=O
1B=2,
∴AH=BH=
.
∴AB=2
.
∴S
菱形AO1BO2=
O
1O
2•AB=2
.
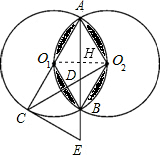
∵AO
1=BO
1=O
2A=O
2B=O
1O
2,
∴△AO
1O
2和△BO
1O
2都是等边三角形.
∴∠AO
2O
1=∠BO
2O
1=60°.
∴∠AO
2B=120°.
同理:∠AO
1B=120°.
∴S
阴影=2(
-2
)=
-4
.
∴图中阴影部分的面积为
-4
.
(3)△AO
2D∽△ACE,相似比为1:2.
证明:∵AC是⊙O
1的直径,
∴∠AO
2C=90°.
∵CE与⊙O
1相切于点C,
∴AC⊥CE,即∠ACE=90°.
∴∠AO
2D=∠ACE=90°.
∵四边形AO
1BO
2是菱形,
∴∠O
2AD=∠CAE.
∴△AO
2D∽△ACE.
其相似比为AO
2:AC=1:2.
点评:本题考查了菱形的判定与性质、相似三角形的判定、扇形的面积公式、菱形的面积公式、勾股定理、切线的性质等知识,考查了用割补法求不规则图形的面积,有一定的综合性.

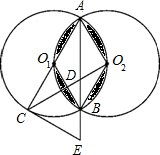 如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.
如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.