
【题目】在△ABC中,BA=BC,∠ABC=α(0°<α<180°),点P为直线BC上一动点(不与点B,C重合),连接AP,将线段PA绕点P顺时针旋转α度得到线段PQ,连接CQ.
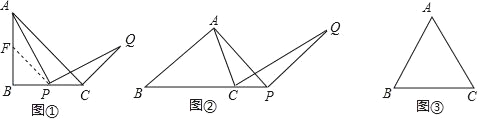
(1)当α=90°,且点P在线段BC上时,过P作PF∥AC交直线AB于点F,如图1,图中与△APF全等的是哪个三角形,∠ACQ的度数.
(2)当点P在BC延长线上,AB:AC=m:n时,如图2,试求线段BP与CQ的比值;
(3)当点P在直线BC上,α=60°,∠APB=30°,CP=4时,请直接写出线段CQ的长.
【答案】(1)△PQC,90;(2)![]() ;(3)线段CQ的长为2或8.
;(3)线段CQ的长为2或8.
【解析】
(1)依据条件判定△APF≌△PQC,可得∠PCQ=∠AFP=135°,依据∠ACB=45°,可得∠ACQ=90°;
(2)过P作PF∥AC,交BA的延长线于F,判定△AFP≌△PCQ,可得FP=CQ,再根据△ABC∽△FBP,可得![]() ,进而得出
,进而得出![]() ;
;
(3)分两种情况进行讨论:点P在CB的延长线上,点P在BC的延长线上,分别依据全等三角形的性质以及含30°角的直角三角形的性质,即可得到线段CQ的长.
(1)如图①,∵∠ABC=90°,AB=CB,
∴△ABC是等腰直角三角形,
∵PF∥AC,
∴∠BPF=∠BFP=45°,
∴△BPF是等腰直角三角形,
∴BF=BP,
∴AF=CP,
由旋转可得,AP=PQ,∠APQ=90°,而∠BPF=45°,
∴∠QPC=45°﹣∠APF,
又∵∠PAF=∠PFB﹣∠APF=45°﹣∠APF,
∴∠PAF=∠QPC,
∴△APF≌△PQC(SAS)
∴∠PCQ=∠AFP=135°,
又∵∠ACB=45°,
∴∠ACQ=90°,
故答案为:△PQC,90;
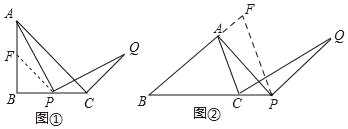
(2)如图②,过P作PF∥AC,交BA的延长线于F,则![]() ,
,
又∵AB=BC,
∴AF=CP,
又∵∠FAP=∠ABC+∠APB=α+∠APB,∠CPQ=∠APQ+∠APB=α+∠APB,
∴∠FAP=∠CPQ,
由旋转可得,PA=PQ,
∴△AFP≌△PCQ(SAS),
∴FP=CQ,
∵PF∥AC,
∴△ABC∽△FBP,
∴![]()
∴![]() ;
;
(3)如图,当P在CB的延长线上时,
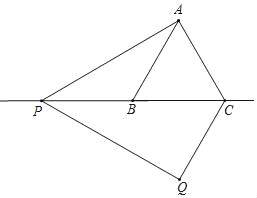
∵∠CPQ=∠APQ﹣∠APB=60°﹣30°=30°,
∴∠APC=∠QPC,
又∵AP=QP,PC=PC,
∴△APC≌△QPC(SAS),
∴CQ=AC,
又∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,∠BAP=∠ABC﹣∠APB=30°,
∴BP=AB=BC=![]() PC=2,
PC=2,
∴QC=AC=BC=2;
如图,当P在BC的延长线上时,连接AQ,
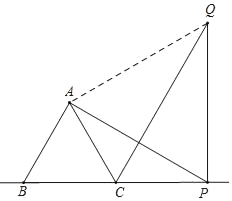
由旋转可得,AP=QP,∠APQ=∠ABC=60°,
∴△APQ是等边三角形,
∴AQ=PQ,∠APQ=60°=∠AQP,
又∵∠APB=30°,∠ACB=60°,
∴∠CAP=30°,∠CPQ=90°,
∴∠CAP=∠APA,
∴AC=PC,且AQ=PQ,CQ=CQ
∴△ACQ≌△PCQ(SSS)
∴∠AQC=∠PQC=![]() ∠AQP=30°,
∠AQP=30°,
∴Rt△PCQ中,CQ=2CP=8.
综上所述,线段CQ的长为2或8.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月热播的专题片《辉煌中国﹣﹣圆梦工程》展示的中国桥、中国路等超级工程展现了中国现代化进程中的伟大成就,大家纷纷点赞“厉害了,我的国!”片中提到我国已成为拥有斜拉桥最多的国家,世界前十座斜拉桥中,中国占七座,其中苏通长江大桥(如图1所示)主桥的主跨长度在世界斜拉桥中排在前列.在图2的主桥示意图中,两座索塔及索塔两侧的斜拉索对称分布,大桥主跨BD的中点为E,最长的斜拉索CE长577m,记CE与大桥主梁所夹的锐角∠CED为α,那么用CE的长和α的三角函数表示主跨BD长的表达式应为BD=_____(m).

查看答案和解析>>
科目:初中数学 来源: 题型:
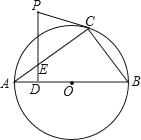
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
(1)求证:∠PCE=∠PEC;
(2)若AB=10,ED=![]() ,sinA=
,sinA=![]() ,求PC的长.
,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
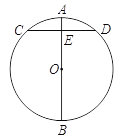
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了在中考体育考试中取得好成绩,每位同学都认真训练,体育成绩也大幅提高,这是从我校某次模拟考试中随机抽取了50名同学的一分钟跳绳次数,并绘制出部分频数分布表和部分频数分布直方图,如下图所示:
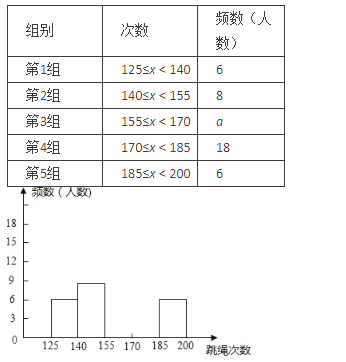
请结合图表完成下列问题:
(1)表中的a= ;
(2)请把频数分布直方图补充完整;
(3)若初三年级共有800名学生,中考体考一分钟跳绳次数大于等于185即为满分20分,根据以上信息,请你估算全年级学生一分钟跳绳次数得满分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.73)
≈1.73)
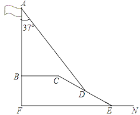
A. 10.61 B. 10.52 C. 9.87 D. 9.37
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com