
°æƒø°øŒ™¡À‘⁄÷–øºÃ”˝øº ‘÷–»°µ√∫√≥…º®£¨√øŒªÕ¨—ß∂º»œ’Ê—µ¡∑£¨Ã”˝≥…º®“≤¥Û∑˘Ã·∏þ£¨’‚ «¥”Œ“–£ƒ≥¥Œƒ£ƒ‚øº ‘÷–Àʪ˙≥È»°¡À50√˚Õ¨—ßµƒ“ª∑÷÷”ï…˛¥Œ ˝£¨≤¢ªÊ÷∆≥ˆ≤ø∑÷∆µ ˝∑÷≤º±Ì∫Õ≤ø∑÷∆µ ˝∑÷≤º÷±∑ΩÕº£¨»Áœ¬ÕºÀ˘ æ£∫
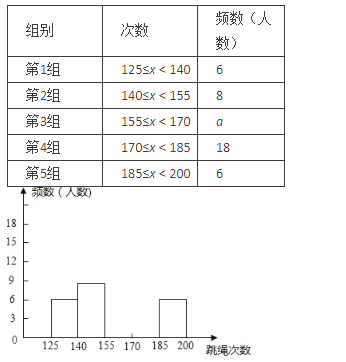
«ÎΩ·∫œÕº±ÌÕÍ≥…œ¬¡–Œ £∫
£®1£©±Ì÷–µƒa£Ω°° °°£ª
£®2£©«Î∞—∆µ ˝∑÷≤º÷±∑ΩÕº≤π≥‰ÕÍ’˚£ª
£®3£©»Ù≥ı»˝ƒÍº∂π≤”–800√˚—ß…˙£¨÷–øºÃÂøº“ª∑÷÷”ï…˛¥Œ ˝¥Û”⁄µ»”⁄185º¥Œ™¬˙∑÷20∑÷£¨∏˘æð“‘…œ–≈œ¢£¨«Îƒ„π¿À„»´ƒÍº∂—ß…˙“ª∑÷÷”ï…˛¥Œ ˝µ√¬˙∑÷µƒ»À ˝£Æ
°æ¥∞∏°ø£®1£©12£Æ£®2£©œÍº˚Ω‚Œˆ£ª£®3£©96£®»À£©£Æ
°æΩ‚Œˆ°ø
£®1£©∏˘æð◊лÀ ˝£Ω∏˜◊È»À ˝÷Æ∫Õ£¨º¥ø…Ω‚æˆŒ £ª
£®2£©3£¨4◊È»À ˝ª≠≥ˆÃı–ŒÕºº¥ø…£ª
£®3£©”√—˘±æπ¿º∆◊ÐõƒÀºœÎº¥ø…Ω‚æˆŒ £ª
Ω‚£∫£®1£©a£Ω50©Å6©Å8©Å18©Å6£Ω12£®»À£©£Æ
π ¥∞∏Œ™12£Æ
£®2£©∆µ ˝∑÷≤º÷±∑ΩÕº»ÁÕºÀ˘ 棨
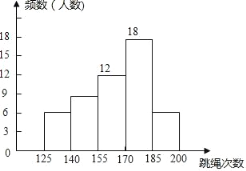
£®3£©≥ı»˝ƒÍº∂π≤”–800√˚—ß…˙£¨µ√¬˙∑÷µƒ»À ˝£Ω800°¡![]() £Ω96£®»À£©£Æ
£Ω96£®»À£©£Æ


 ≥Â¥Ã100∑÷µ•‘™”≈ªØ¡∑øºæÌœµ¡–¥∞∏
≥Â¥Ã100∑÷µ•‘™”≈ªØ¡∑øºæÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝y=ax2+bx+c(a°Ÿ0)µƒÕºœÛ»ÁÕºÀ˘ 棨∂‘≥∆÷·Œ™÷±œþ![]() .œ¬¡–Ω·¬€÷–£¨’˝»∑µƒ «£®°°°°£©
.œ¬¡–Ω·¬€÷–£¨’˝»∑µƒ «£®°°°°£©

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘À∂Ø‘±Ω´–°«Ú—ÿ”εÿ√Ê≥…“ª∂®Ω«∂»µƒ∑ΩœÚª˜≥ˆ£¨‘⁄≤ªøº¬«ø’∆¯◊Ë¡¶µƒÃıº˛œ¬£¨–°«Úµƒ∑…––∏þ∂»h£®m£©”ÎÀ¸µƒ∑…–– ±º‰t£®s£©¬˙◊„∂˛¥Œ∫Ø ˝πÿœµ£¨t”Îhµƒº∏◊È∂‘”¶÷µ»Áœ¬±ÌÀ˘ æ£Æ
t£®s£© | 0 | 0.5 | 1 | 1.5 | 2 | °≠ |
h£®m£© | 0 | 8.75 | 15 | 18.75 | 20 | °≠ |
£®1£©«Ûh”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£®≤ª“™«Û–¥tµƒ»°÷µ∑∂Œß£©£ª
£®2£©«Û–°«Ú∑…––3s ±µƒ∏þ∂»£ª
£®3£©Œ £∫–°«Úµƒ∑…––∏þ∂»ƒÐ∑Ò¥ÔµΩ22m£ø«ÎÀµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
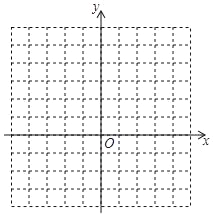
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ Ω «y£Ωx2©Å2x©Å3£Æ
£®1£©”Îy÷·µƒΩªµ„◊¯±Í «°° °°£¨∂•µ„◊¯±Í «°° °°£Æ
£®2£©‘⁄◊¯±Íœµ÷–¿˚”√√˵„∑®ª≠≥ˆ¥À≈◊ŒÔœþ£ª
x | °≠ | °≠ | |||||
y | °≠ | °≠ |
£®3£©Ω·∫œÕºœÛªÿ¥£∫µ±©Å2£ºx£º2 ±£¨∫Ø ˝÷µyµƒ»°÷µ∑∂Œß «°° °°£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
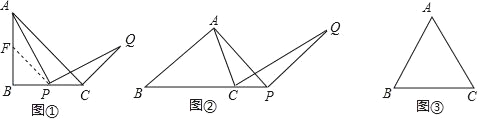
°æƒø°ø‘⁄°˜ABC÷–£¨BA£ΩBC£¨°œABC£Ω¶¡£®0°„£º¶¡£º180°„£©£¨µ„PŒ™÷±œþBC…œ“ª∂ص„£®≤ª”ε„B£¨C÷ÿ∫œ£©£¨¡¨Ω”AP£¨Ω´œþ∂ŒPA»∆µ„PÀ≥ ±’Ζ˝◊™¶¡∂»µ√µΩœþ∂ŒPQ£¨¡¨Ω”CQ£Æ
£®1£©µ±¶¡£Ω90°„£¨«“µ„P‘⁄œþ∂ŒBC…œ ±£¨π˝P◊˜PF°ŒACΩª÷±œþAB”⁄µ„F£¨»ÁÕº1£¨Õº÷–”ΰ˜APF»´µ»µƒ «ƒƒ∏ˆ»˝Ω«–Œ£¨°œACQµƒ∂» ˝£Æ
£®2£©µ±µ„P‘⁄BC—”≥§œþ…œ£¨AB£∫AC£Ωm£∫n ±£¨»ÁÕº2£¨ ‘«Ûœþ∂ŒBP”ÎCQµƒ±»÷µ£ª
£®3£©µ±µ„P‘⁄÷±œþBC…œ£¨¶¡£Ω60°„£¨°œAPB£Ω30°„£¨CP£Ω4 ±£¨«Î÷±Ω”–¥≥ˆœþ∂ŒCQµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº¢Ÿ£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœþy£Ωax2+bx+4![]() ”Îx÷·Ωª”⁄A£¨B¡Ωµ„£®µ„A‘⁄µ„B◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„C£¨≈◊ŒÔœþµƒ∂•µ„Œ™µ„D£¨«“3OC£Ω4OB£¨∂‘≥∆÷·Œ™÷±œþx£Ω
”Îx÷·Ωª”⁄A£¨B¡Ωµ„£®µ„A‘⁄µ„B◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„C£¨≈◊ŒÔœþµƒ∂•µ„Œ™µ„D£¨«“3OC£Ω4OB£¨∂‘≥∆÷·Œ™÷±œþx£Ω![]() £¨µ„E
£¨µ„E![]() £¨¡¨Ω”CEΩª∂‘≥∆÷·”⁄µ„F£¨¡¨Ω”AFΩª≈◊ŒÔœþ”⁄µ„G£Æ
£¨¡¨Ω”CEΩª∂‘≥∆÷·”⁄µ„F£¨¡¨Ω”AFΩª≈◊ŒÔœþ”⁄µ„G£Æ
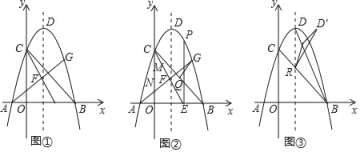
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω∫Õ÷±œþCEµƒΩ‚Œˆ Ω£ª
£®2£©»ÁÕº¢⁄£¨π˝E◊˜EP°Õx÷·Ωª≈◊ŒÔœþ”⁄µ„P£¨µ„Q «œþ∂ŒBC…œ“ª∂ص„£¨µ±QG+![]() QB◊Ó–° ±£¨œþ∂ŒMN‘⁄œþ∂ŒCE…œ“∆∂Ø£¨µ„M‘⁄µ„N…œ∑Ω£¨«“MN£Ω
QB◊Ó–° ±£¨œþ∂ŒMN‘⁄œþ∂ŒCE…œ“∆∂Ø£¨µ„M‘⁄µ„N…œ∑Ω£¨«“MN£Ω![]() £¨«Î«Û≥ˆÀƒ±þ–ŒPQMN÷Ð≥§◊Ó–° ±µ„Nµƒ∫·◊¯±Í£ª
£¨«Î«Û≥ˆÀƒ±þ–ŒPQMN÷Ð≥§◊Ó–° ±µ„Nµƒ∫·◊¯±Í£ª
£®3£©»ÁÕº¢€£¨BC”Î∂‘≥∆÷·Ωª”⁄µ„R£¨¡¨Ω”BD£¨µ„S «œþ∂ŒBD…œ“ª∂ص„£¨Ω´°˜DRS—ÿ÷±œþRS’€µ˛÷¡°˜D°‰RS£¨ «∑ҥʑ⁄µ„S πµ√°˜D°‰RS”ΰ˜BRS÷ÿµ˛≤ø∑÷µƒÕº–Œ «÷±Ω«»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆBSµƒ≥§£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ£®≤Œøº ˝æð£∫tan°œDBC£Ω![]() £©
£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø °…‰ª˜∂”Œ™¥”º◊°¢““¡Ω√˚‘À∂Ø‘±÷–—°∞Œ“ª»À≤Œº”»´π˙±»»¸£¨∂‘À˚√«Ω¯––¡À¡˘¥Œ≤‚ ‘£¨≤‚ ‘≥…º®»Áœ¬±Ì£®µ•Œª£∫ª∑£©£∫
µ⁄“ª¥Œ | µ⁄∂˛¥Œ | µ⁄»˝¥Œ | µ⁄Àƒ¥Œ | µ⁄ŒÂ¥Œ | µ⁄¡˘¥Œ | |
º◊ | 10 | 8 | 9 | 8 | 10 | 9 |
““ | 10 | 7 | 10 | 10 | 9 | 8 |
£®1£©∏˘æð±Ì∏Ò÷–µƒ ˝æ𣨺∆À„≥ˆº◊µƒ∆Ωæ˘≥…º® « ª∑£¨““µƒ∆Ωæ˘≥…º® « ª∑£ª
£®2£©∑÷±º∆À„º◊°¢““¡˘¥Œ≤‚ ‘≥…º®µƒ∑Ω≤Ó£ª
£®3£©∏˘æð£®1£©°¢£®2£©º∆À„µƒΩ·π˚£¨ƒ„»œŒ™Õ∆ºˆÀ≠≤Œº”»´π˙±»»¸∏¸∫œ £¨«ÎÀµ√˜¿Ì”…£Æ
º∆À„∑Ω≤Óµƒπ´ Ω£∫s2£Ω![]() [(x1£≠
[(x1£≠![]() )2£´(x2£≠
)2£´(x2£≠![]() )2£´£´(xn£≠
)2£´£´(xn£≠![]() )2]
)2]
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øAD «µ»—¸°˜ABC÷–BC±þ…œµƒ∏þ£¨«“AD£Ω![]() BC£¨«ÎÕ®π˝ª≠Õº«Û≥ˆ°œABCÀ˘”–ø…ƒÐµƒ÷µ£Æ
BC£¨«ÎÕ®π˝ª≠Õº«Û≥ˆ°œABCÀ˘”–ø…ƒÐµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
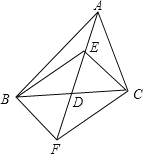
°æƒø°ø‘⁄°˜ABC ÷–£¨D « BC ±þµƒ÷–µ„£¨E°¢F ∑÷±‘⁄ AD º∞∆‰—”≥§œþ…œ£¨CE°ŒBF£¨¡¨Ω”BE°¢CF£Æ
£®1£©«Û÷§£∫°˜BDF °’°˜CDE£ª
£®2£©»Ù DE = BC£¨ ‘≈–∂œÀƒ±þ–Œ BFCE «‘ı—˘µƒÀƒ±þ–Œ£¨≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
BC£¨ ‘≈–∂œÀƒ±þ–Œ BFCE «‘ı—˘µƒÀƒ±þ–Œ£¨≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com