
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=�� ![]() x2+bx+c��x�ύ��A��D���㣬��y�ύ�ڵ�B���ı���OBCD�Ǿ��Σ���A������Ϊ��1��0������B������Ϊ��0��4������֪��E��m��0�����߶�DO�ϵĶ��㣬����E��PE��x�ύ�������ڵ�P����BC�ڵ�G����BD�ڵ�H��
x2+bx+c��x�ύ��A��D���㣬��y�ύ�ڵ�B���ı���OBCD�Ǿ��Σ���A������Ϊ��1��0������B������Ϊ��0��4������֪��E��m��0�����߶�DO�ϵĶ��㣬����E��PE��x�ύ�������ڵ�P����BC�ڵ�G����BD�ڵ�H��
��1����������ߵĽ���ʽ��
��2������P��ֱ��BC�Ϸ�ʱ�����ú�m�Ĵ���ʽ��ʾPG�ij��ȣ�
��3���ڣ�2���������£��Ƿ���������ĵ�P��ʹ����P��B��GΪ��������������DEH���ƣ������ڣ������ʱm��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��������y=�� ![]() x2+bx+c��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B��0��4����
x2+bx+c��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B��0��4����
��  �����
�����  ��
��
�������ߵĽ���ʽΪy=�� ![]() x2��
x2�� ![]() x+4
x+4

��2��
�⣺��E��m��0����B��0��4����PE��x�ύ�������ڵ�P����BC�ڵ�G��
��P��m���� ![]() m2��
m2�� ![]() m+4����G��m��4����
m+4����G��m��4����
��PG=�� ![]() m2��
m2�� ![]() m+4��4=��
m+4��4=�� ![]() m2��
m2�� ![]() m��
m��
��P��ֱ��BC�Ϸ�ʱ������Ҫ�����������ֱ��BC�Ľ��㣬
��4=�� ![]() m2��
m2�� ![]() m+4�����m=��2��0��
m+4�����m=��2��0��
��m��ȡֵ��Χ����2��m��0��
PG�ij������� ![]() m2��
m2�� ![]() m����2��m��0��
m����2��m��0��
��3��
�⣺�ڣ�2���������£����ڵ�P��ʹ����P��B��GΪ��������������DEH���ƣ�
��y=�� ![]() x2��
x2�� ![]() x+4��
x+4��
�൱y=0ʱ���� ![]() x2��
x2�� ![]() x+4=0��
x+4=0��
���x=1��3��
��D����3��0����
����P��ֱ��BC�Ϸ�ʱ����2��m��0��
��ֱ��BD�Ľ���ʽΪy=kx+4��
��D����3��0�����룬�é�3k+4=0��
���k= ![]() ��
��
��ֱ��BD�Ľ���ʽΪy= ![]() x+4��
x+4��
��H��m�� ![]() m+4����
m+4����
�����������
�������BGP�ס�DEH����ô ![]() ��
��
�� ![]() =
=  ��
��
���m=��3��1��
�ɩ�2��m��0����m=��1��
�������PGB�ס�DEH����ô ![]() ��
��
�� ![]() =
= ![]() ��
��
�ɩ�2��m��0�����m=�� ![]() ��
��
�����������ڣ�2���������£����ڵ�P��ʹ����P��B��GΪ��������������DEH���ƣ���ʱm��ֵΪ��1�� ![]() ��
��
����������1����A��1��0����B��0��4������y=�� ![]() x2+bx+c�����ô���ϵ����������������ߵĽ���ʽ����2����E��m��0����B��0��4�����ó�P��m����
x2+bx+c�����ô���ϵ����������������ߵĽ���ʽ����2����E��m��0����B��0��4�����ó�P��m���� ![]() m2��
m2�� ![]() m+4����G��m��4������PG=��
m+4����G��m��4������PG=�� ![]() m2��
m2�� ![]() m+4��4=��
m+4��4=�� ![]() m2��
m2�� ![]() m����P��ֱ��BC�Ϸ�ʱ������Ҫ���m��ȡֵ��Χ����3�����������ߵĽ���ʽ���D����3��0������P��ֱ��BC�Ϸ�ʱ����2��m��0�������ô���ϵ�������ֱ��BD�Ľ���ʽΪy=
m����P��ֱ��BC�Ϸ�ʱ������Ҫ���m��ȡֵ��Χ����3�����������ߵĽ���ʽ���D����3��0������P��ֱ��BC�Ϸ�ʱ����2��m��0�������ô���ϵ�������ֱ��BD�Ľ���ʽΪy= ![]() x+4�����ǵó�H��m��
x+4�����ǵó�H��m�� ![]() m+4��������P��B��GΪ��������������DEH����ʱ�����ڡ�PGB=��DEH=90�㣬���Է���������������ۣ��١�BGP�ס�DEH���ڡ�PGB�ס�DEH�������Ը������������ζ�Ӧ�߳ɱ����г�������ϵʽ���������m��ֵ��
m+4��������P��B��GΪ��������������DEH����ʱ�����ڡ�PGB=��DEH=90�㣬���Է���������������ۣ��١�BGP�ס�DEH���ڡ�PGB�ס�DEH�������Ը������������ζ�Ӧ�߳ɱ����г�������ϵʽ���������m��ֵ��
�����㾫�������ڱ��⿼��Ķ��κ��������ʣ���Ҫ�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С���ܵó���ȷ�𰸣�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=40�㣬AB�Ĵ�ֱƽ����MN��AC�ڵ�D����DBC=30�㣬��AB=m��BC=n�����DBC���ܳ�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=40�㣬AB�Ĵ�ֱƽ����MN��AC�ڵ�D����DBC=30�㣬��AB=m��BC=n�����DBC���ܳ�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����������ͬ·��ǰ�����뵥λ10km����ѵ���IJμ�ѧϰ��ͼ��l����l���ֱ��ʾ�ס�������ǰ��Ŀ�ĵ����ߵ�·��S��km����ʱ��t���֣��仯�ĺ���ͼ������˵����
���ұȼ���ǰ12���ӵ��
����ƽ���ٶ�Ϊ15ǧ��/Сʱ��
��������8km�������ף�
���ҳ���6���Ӻ��ϼף�
������ȷ���У� ��
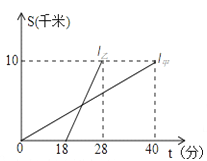
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B����ͬʱ��ԭ��O��������A��ÿ��x����λ������x��ĸ������˶�����B��ÿ��y����λ������y����������˶���
��1����|x+2y��5|+|2x��y|=0���Էֱ����1���Ӻ�A��B��������ꣻ

��2�����BAO����Ǻ͡�ABO����ǵ�ƽ�����ཻ�ڵ�P���ʣ���A��B���˶��Ĺ����У���P�Ĵ�С�Ƿ�ᷢ���仯�����������仯���������ֵ���������仯����˵����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�ĸ��߶��ӳ�һ����A�䡢B�䡢C����������Щ�㣬�õ�һ���µ���������A��B��C��������ABC�����Ϊ1������A��B��C��������ǣ� ��

A. 4 B. 5 C. 6 D. 7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������ABDƽ�ƣ�ʹD��BD�ӳ�������C�õ���A��B��D�䣬A��B�佻AC��E��ADƽ����BAC��

��1��������B��EC����A��֮��Ĺ�ϵ����д�����ɣ�
��2����ͼ����ABDƽ������ͼ��2����ʾ���õ���A��B��D�䣬���ʣ�A��Dƽ����B��A��C��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨����a��b֮���һ�����㣬����(a��b)�����![]() ����ô(a��b)=c��
����ô(a��b)=c��
���磺��Ϊ23=8������(2��8)=3��
��1�����������涨����գ�
��3��27��=_______����5��1��=_______����2�� ![]() ��=_______��
��=_______��
��2��С�����о���������ʱ����һ������3n��4n��=��3��4��С�����������µ�֤����
�裨3n��4n��=x����3n��x=4n������3x��n=4n
����3x=4������3��4��=x��
���ԣ�3n��4n��=��3��4����
���㳢�������������ַ���˵�����������ʽ���������ɣ�(4��5)+(4��6)=(4��30)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com