
【题目】如图(1)将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC.

(1)猜想∠B′EC与∠A′之间的关系,并写出理由.
(2)如图将△ABD平移至如图(2)所示,得到△A′B′D′,请问:A′D平分∠B′A′C吗?为什么?
【答案】(1)∠B′EC=2∠A′;(2)A′D′平分∠B′A′C.见解析
【解析】
试题分析:(1)根据平移的性质得出∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,进而得出∠BAC=∠B′EC,进而得出答案;
(2)利用平移的性质得出∠B′A′D′=∠BAD,AB∥A′B′,进而得出∠BAD=![]() ∠BAC,即可得出∠B′A′D′=
∠BAC,即可得出∠B′A′D′=![]() ∠B′A′C.
∠B′A′C.
解:(1)∠B′EC=2∠A′,
理由:∵将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC,
∴∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,
∴∠BAC=∠B′EC,
∴∠BAD=∠A′=![]() ∠BAC=
∠BAC=![]() ∠B′EC,
∠B′EC,
即∠B′EC=2∠A′;
(2)A′D′平分∠B′A′C,
理由:∵将△ABD平移至如图(2)所示,得到△A′B′D′,
∴∠B′A′D′=∠BAD,AB∥A′B′,
∴∠BAC=∠B′A′C,
∵∠BAD=![]() ∠BAC,
∠BAC,
∴∠B′A′D′=![]() ∠B′A′C,
∠B′A′C,
∴A′D′平分∠B′A′C.


科目:初中数学 来源: 题型:
【题目】这个周末,七年级准备组织观看电影《我和我的祖国》,由各班班长负责买票,一班班长问售票员买团体票是否可以优惠,售票员说:50人以上的团体票有两个优惠方案可选择:
方案一:全体人员可打8折;
方案二:若打9折,有6人可以免票.
一班班长思考了一会儿,说我们班无论选择哪种方案要付的钱是一样的,请问一班有几人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣ ![]() x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
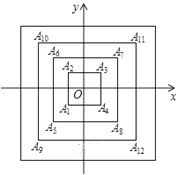
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用![]() ,
,![]() ,
,![]() ,
,![]() …表示,则顶点
…表示,则顶点![]() 的坐标是_____.
的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC与三角形A'B'C'在平面直角坐标系中的位置如图:
(1)分别写出下列各点的坐标:A'_____; B'_____;C'_____;
(2)三角形A'B'C'由三角形ABC经过怎样的平移得到?___________;
(3)若点P(a,b)是三角形ABC内部一点,则平移后三角形A'B'C'内的对应点P'的坐标为_________;
(4)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1 ,2).
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',则△A'B'C'的三个顶点坐标分别是A'( , )、B'( 、 )、 C'( 、 )

(3)计算△ABC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com