
【题目】如图①,△ABC中,AC=BC,∠A=30°,点D在AB边上且∠ADC=45°.
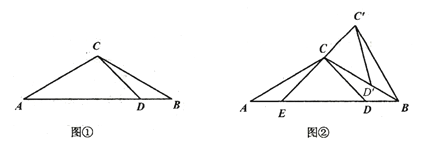
(1)求∠BCD的度数;
(2)将图①中的△BCD绕点B顺时针旋转,得到△BC′D′.当点D′恰好落在BC边上时,如图②所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
【答案】(1)15°;(2)①75°;②答案见解析.
【解析】试题分析:(1)根据三角形外角性质,即可得到∠BCD=∠ADC﹣∠CBA=15°;
(2)①由旋转可得CB=C'B=AC,∠C'BD'=∠CBD=∠A=30°,再根据等腰三角形的性质,即可得到∠CC'B=∠C'CB=75°;
②先根据AC=C'B,∠C'BD'=∠A,得出∠CEB=∠C'CB﹣∠CBA=45°,进而得到∠ACE=∠CEB﹣∠A=15°,据此可得∠BC'D'=∠BCD=∠ACE,运用ASA即可判定△C'BD'≌△CAE.
试题解析:解:(1)∵AC=BC,∠A=30°,∴∠CBA=∠CAB=30°.∵∠ADC=45°,∴∠BCD=∠ADC﹣∠CBA=15°=∠BC'D';
(2)①由旋转可得CB=C'B=AC,∠C'BD'=∠CBD=∠A=30°,∴∠CC'B=∠C'CB=75°;
②证明:∵AC=C'B,∠C'BD'=∠A,∴∠CEB=∠C'CB﹣∠CBA=45°,∴∠ACE=∠CEB﹣∠A=15°,∴∠BC'D'=∠BCD=∠ACE.在△C'BD'和△CAE中,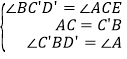 ,∴△C'BD'≌△CAE(ASA).
,∴△C'BD'≌△CAE(ASA).


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点A、B的横坐标分别为﹣3、1,与y轴交于点C,下面四个结论:①16a+4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣
,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣![]() 或﹣
或﹣![]() .其中正确的有_____.(请将正确结论的序号全部填在横线上)
.其中正确的有_____.(请将正确结论的序号全部填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段![]() 上.点P从点C出发向点
上.点P从点C出发向点![]() 运动,速度为2cm/s;同时,点Q也从点C以4cm/s速度出发用1s到达A处,并在A处停留2s,然后按原速度向点B运动,.最终,点Q比点P早1s到达B处.设点P运动的时间为t.
运动,速度为2cm/s;同时,点Q也从点C以4cm/s速度出发用1s到达A处,并在A处停留2s,然后按原速度向点B运动,.最终,点Q比点P早1s到达B处.设点P运动的时间为t.
(1)线段AC的长为 cm;当t=3s时,P,Q两点之间的距离为 cm;
(2)求线段BC的长;
(3)从P,Q两点同时出发至点P到达点B处的这段时间内,t为何值时,P,Q两点相距1cm?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.请根据图中的信息,解答下列问题:

(1)在这次调查中,一共抽取了________名学生,a=________%;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为________度;
(4)若该校共有2 000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇在周日上午8:00从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心
接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/时的平均速
度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原
路返回.设小宇离家 x 小时后,到达离家y千米的地方,图中折线OABCD表示 y 与 x 之间的函数关系.下
列叙述错误的是( )
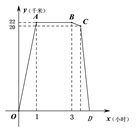
A. 活动中心与小宇家相距22千米
B. 小宇在活动中心活动时间为2小时
C. 他从活动中心返家时,步行用了0.4小时
D. 小宇不能在12:00前回到家
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠C=90°,CA=CB=4![]() cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数
cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
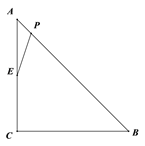
下面是小安的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 2.8 | 2.2 | 2.0 | 2.2 | 2.8 | 3.6 | 5.4 | 6.3 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①写出该函数的一条性质: ;
②当![]() 时,
时,![]() 的长度约为 cm.
的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形ABCD的顶点B在坐标原点,顶点A、C分别在y轴、x轴的负半轴上,其中![]() ,
,![]() ,将矩形ABCD绕点D逆时针旋转得到矩形
,将矩形ABCD绕点D逆时针旋转得到矩形![]() ,点
,点![]() 恰好落在x轴上,线段
恰好落在x轴上,线段![]() 与CD交于点E,那么点E的坐标为
与CD交于点E,那么点E的坐标为![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价位500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=﹣x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)档这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
【答案】(1)取值范围为1100元/人~1200元/人之间;(2)50000;(3)x=900时,w最大=160000
【解析】试题分析:(1)根据题意列不等式求解可;
(2)根据报价减去成本可得到函数的解析式,根据一次函数的图像求解即可;
(3)根据利润等于人次乘以价格即可得到函数的解析式,然后根据二次函数的最值求解即可.
试题解析:(1)∵由题意得![]() 时,即
时,即![]() ,
,
∴解得![]()
即要将该旅游线路每月游客人数控制在200人以内,该旅游线路报价的取值范围为1100元/人~1200元/人之间;
(2)![]() ,
,![]() ,∴
,∴![]()
∵![]() ,∴当
,∴当![]() 时,z最低,即
时,z最低,即![]() ;
;
(3)利润![]()
当![]() 时,
时,![]() .
.
【题型】解答题
【结束】
23
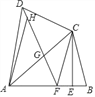
【题目】已知四边形ABCD中,AB=AD,对角线AC平分∠DAB,过点C作CE⊥AB于点E,点F为AB上一点,且EF=EB,连接DF.
(1)求证:CD=CF;
(2)连接DF,交AC于点G,求证:△DGC∽△ADC;
(3)若点H为线段DG上一点,连接AH,若∠ADC=2∠HAG,AD=3,DC=2,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com